Main Page
Welcome to the ApCoCoA Website
ApCoCoA (Applied Computations in Computer Algebra) is a computer algebra framework based on the computer algebra system CoCoA. In this Wiki you can find the complete ApCoCoA manual, the newest versions and useful How To's around ApCoCoA and its packages.
What is CoCoA?
Latest Version: CoCoA-5.4.0 (11.04.2022)
CoCoA is a computer algebra software for computations with multivariate polynomial rings. Information about functions in CoCoA-5 can be found in the official CoCoA-5 Manual. More information about CoCoA itself can be found on http://cocoa.dima.unige.it/.
Originally, this Wiki was designed to contain manual pages for CoCoA-4, an earlier version of CoCoA. The articles concerning CoCoA-4 can be found in the CoCoA section of this Wiki and Category:CoCoA4.
Although CoCoA-4 can still be downloaded, it is no longer developed since CoCoA-5 was released in June 2011 with a new syntax and a technically advanced implementation in C++.
What about ApCoCoA-1?
Latest Version: ApCoCoA-1.9.1 (11.10.2013)
ApCoCoA-1 was the predecessor of ApCoCoA-2 based on CoCoA-4. In brief, ApCoCoA-1 is CoCoA-4 wrapped in an Eclipse GUI and provided with a lot of additional functionalities like extra packages and access from CoCoA-4 code to external libraries like GLPK, Gnuplot, CryptoMiniSat and many more. For a detailed description and a full list of provided functionalities, see What is ApCoCoA. For a manual, see ApCoCoA-1 Manual.
After the end of the developement of CoCoA-4, ApCoCoA-1 soon also stopped being developed.
What is ApCoCoA-2?
Latest Version: ApCoCoA-2.0 (06.03.2023)
ApCoCoA-2 is a Computer Algebra Framework based on CoCoA-5. ApCoCoA-2 is basically CoCoA-5 extended by some packages and functionalities and wrapped in an IntelliJ GUI.
For installing ApCoCoA-2, go to the ApCoCoA Download Page and follow the instructions.
A list and documentations of available packages, see the package list containing all ApCoCoA-2 packages, which are documented in this Wiki. Informations about the CoCoA syntax can be looked up in the official CoCoA Manual.
What is CoCoALib?
CoCoALib is a C++ library for doing computations in Commutative Algebra. It is the kernel of CoCoA-5 and can be downloaded from the official CoCoA website.
What is ApCoCoALib?
ApCoCoALib is a C++ library extending CoCoALib. It is included in ApCoCoA and can be accessed through the ApCoCoA Server.
Contribute
ApCoCoA is developed by the ApCoCoA Team, which is lead by Martin Kreuzer. Since we are a small team and there is much to do, new contributors are always welcome. If you want to help with the Wiki, you need to get an account, so please contact one of our team members who is working on the Wiki about creating an account for you. Contact Details can be found at the website of the Chair of Symbolic Computation at the University of Passau.
In order to contribute a package to ApCoCoA-2, please follow the steps described in HowTo:Contribute an ApCoCoA-2 Package. There you get all informations about how to write a package and how to document it in the Wiki. A list of requested Packages can be found at ApCoCoAWiki:Requested Packages.
A to-do list especially for this Wiki can be found at ApCoCoAWiki:Todo. If you are familiar with CoCoA and want to write How To's, then you can go to ApCoCoAWiki:Requested HowTo's for a list of requested HowTo's.
If you have any questions, concerns or suggestions about ApCoCoA and this Wiki, please do not hesitate to contact us.
Application Examples
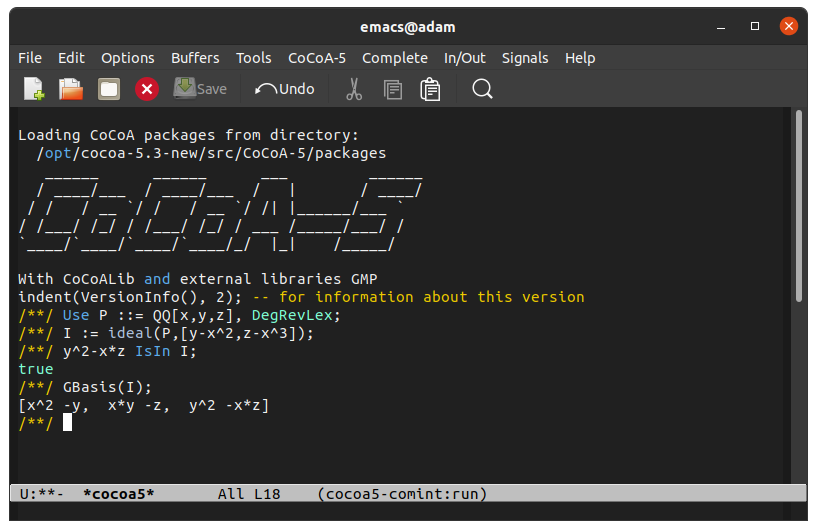
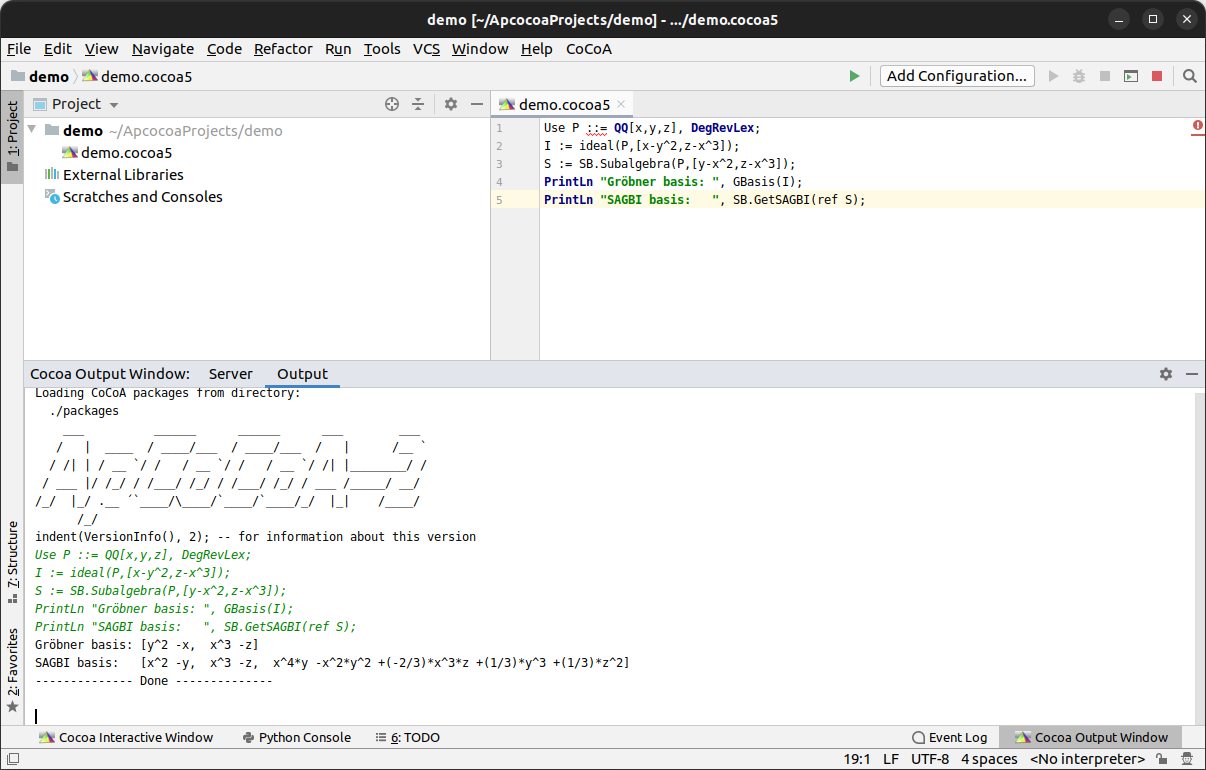
Computing reduced Gröbner bases:
Use P ::= QQ[x,y,z], DegRevLex; I := ideal(P,[y-x^2,z-x^3]); GBasis(I); -- reduced DegRevLex Gröbner basis of I
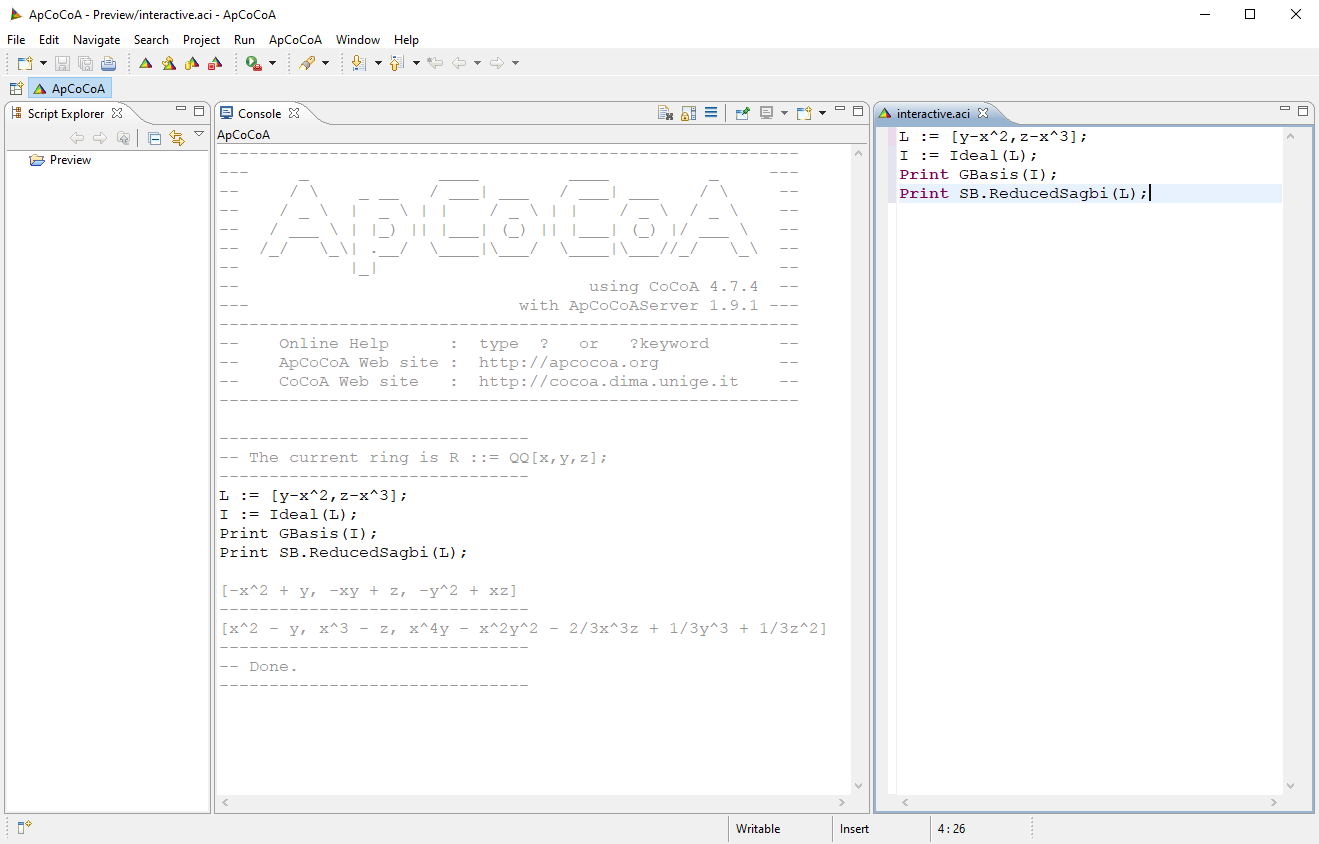
Computing reduced SAGBI bases:
Use P ::= QQ[x,y,z], DegLex; S := SB.Subalgebra(P,[y-x^2,z-x^3]); SB.SAGBI(S); -- reduced DegLex-SAGBI basis of S
Solving polynomial equations over using a SAT solver:
Use ZZ/(2)[x,y,z]; f1 := x*y + x*z + y*z + z; f2 := y + 1; f3 := x*y + z; SAT.Solve([f1,f2,f3]); -- [0, 1, 0]
News and Appointments
- 2023/03/19 - 2023/03/25: CoCoA School in Hue, Vietnam
- 2023/03/06: Release of new and improved ApCoCoA-2.0: Download
- 2020/02/26: Release of ApCoCoA-2.0 Beta based on CoCoA 5 and with a new IntelliJ interface