Difference between revisions of "ApCoCoA-1:GLPK.MIPSolve"
m |
|||
| Line 3: | Line 3: | ||
<short_description>solve linear programms</short_description> | <short_description>solve linear programms</short_description> | ||
<syntax> | <syntax> | ||
| − | GLPK.MIPSolve( | + | GLPK.MIPSolve(Objective_f:POLYNOM, EQ_Polynomials:LIST, LE_Polynomials:LIST, GE_Polynomials:LIST, Bounds:LIST, IntNum:LIST, Binaries:LIST, MinMax:STRING) |
</syntax> | </syntax> | ||
<description> | <description> | ||
{{ApCoCoAServer}} | {{ApCoCoAServer}} | ||
| − | <em> | + | <em>Objective_f</em>: A linear polynomial which is equivalent to the linear objective function. |
<em>EQ_Polynomials</em>: List of linear polynomials, which are equivalent to the equality-part in the list of conditions. | <em>EQ_Polynomials</em>: List of linear polynomials, which are equivalent to the equality-part in the list of conditions. | ||
Revision as of 20:25, 30 November 2008
LPSolve
solve linear programms
Syntax
GLPK.MIPSolve(Objective_f:POLYNOM, EQ_Polynomials:LIST, LE_Polynomials:LIST, GE_Polynomials:LIST, Bounds:LIST, IntNum:LIST, Binaries:LIST, MinMax:STRING)
Description
Please note: The function(s) explained on this page is/are using the ApCoCoAServer. You will have to start the ApCoCoAServer in order to use
it/them.
Objective_f: A linear polynomial which is equivalent to the linear objective function.
EQ_Polynomials: List of linear polynomials, which are equivalent to the equality-part in the list of conditions.
LE_Polynomials: List of linear polynomials, which are equivalent to the lower or equal-part in the list of conditions.
GE_Polynomials: List of linear polynomials, which are equivalent to the greater or equal-part in the list of conditions.
Bounds: List of lists with two elements. Each List contains the lower and upper bounds for each variable. You can choose between INT or RAT for the type of each bound, if you type in a (empty) string, then it means minus infinity (first place) or plus infinity (second place).
IntNum: List of variables, which should be integer.
Binaries: List of variables, which are binaries (0 or 1).
MinMax: Minimization (Min) or maximization (Max), that's the question.
Specification of the paths: When you execute the GLPK.LPSolve-command, you had to specify the path of the LP solver glpsol, i.e. GlpsolPath:="/usr/bin/";
and the working path, i.e. WorkingPath:="/home/user/";
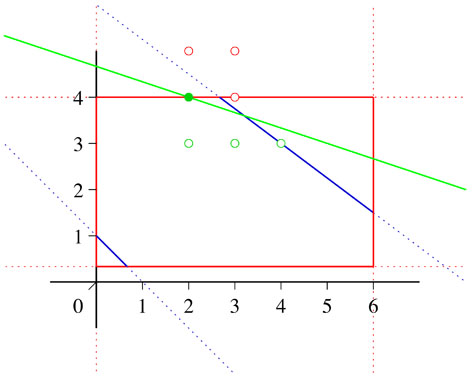
First we want to discuss a rather easy example.
Example
We want to maximize the Function y = - 1/2x, with the two conditions y ≤ 6 - 3/4x and y ≥ 1 - x and the bounds 0 ≤ x ≤ 6 and 1/3 ≤ y ≤ 4. We prename the input of GLPK.LPSol-function. OF := 1/2x + y; LE := 3/4x + y - 6; GE := x + y - 1; Bounds:=[[0,6], [1/3,4]]; IntNum:=[x,y] Then we compute the solution with Use S::=Q[x,y]; $GLPK.MIPSolve(OF, LE, GE, Bounds, IntNum, [], "Max"); And we achieve x = 2 and y = 4.
Example
''Linear programming example 1996 MBA exam'' A cargo plane has three compartments for storing cargo: front, centre and rear. These compartments have the following limits on both weight and space: Compartment Weight capacity (tonnes) Space capacity (cubic metres) Front 10 6800 Centre 16 8700 Rear 8 5300 Furthermore, the weight of the cargo in the respective compartments must be the same proportion of that compartment's weight capacity to maintain the balance of the plane. The following four cargoes are available for shipment on the next flight: Cargo Weight (tonnes) Volume (cubic metres/tonne) Profit (£/tonne) C1 18 480 310 C2 15 650 380 C3 23 580 350 C4 12 390 285 Any proportion of these cargoes can be accepted. The objective is to determine how much (if any) of each cargo C1, C2, C3 and C4 should be accepted and how to distribute each among the compartments so that the total profit for the flight is maximised. To solve this problem we had to compose a linear program. Variables We need to decide how much of each of the four cargoes to put in each of the three compartments. Hence let: xij be the number of tonnes of cargo i (i=1,2,3,4 for C1, C2, C3 and C4 respectively) that is put into compartment j (j=1 for Front, j=2 for Centre and j=3 for Rear) where xij >=0 i=1,2,3,4; j=1,2,3 Note here that we are explicitly told we can split the cargoes into any proportions (fractions) that we like. Constraints * cannot pack more of each of the four cargoes than we have available x11 + x12 + x13 ≤ 18 x21 + x22 + x23 ≤ 15 x31 + x32 + x33 ≤ 23 x41 + x42 + x43 ≤ 12 * the weight capacity of each compartment must be respected x11 + x21 + x31 + x41 ≤ 10 x12 + x22 + x32 + x42 ≤ 16 x13 + x23 + x33 + x43 ≤ 8 * the volume (space) capacity of each compartment must be respected 480x11 + 650x21 + 580x31 + 390x41 ≤ 6800 480x12 + 650x22 + 580x32 + 390x42 ≤ 8700 480x13 + 650x23 + 580x33 + 390x43 ≤ 5300 * the weight of the cargo in the respective compartments must be the same proportion of that compartment's weight capacity to maintain the balance of the plane [x11 + x21 + x31 + x41]/10 = [x12 + x22 + x32 + x42]/16 = [x13 + x23 + x33 + x43]/8 Objective The objective is to maximise total profit, i.e. maximise 310[x11+ x12+x13] + 380[x21+ x22+x23] + 350[x31+ x32+x33] + 285[x41+ x42+x43] The basic assumptions are: * that each cargo can be split into whatever proportions/fractions we desire * that each cargo can be split between two or more compartments if we so desire * that the cargo can be packed into each compartment (for example if the cargo was spherical it would not be possible to pack a compartment to volume capacity, some free space is inevitable in sphere packing) * all the data/numbers given are accurate In ApCoCoa you can solve this LP like this: Use S::= Q[x[1..4,1..3]]; Objective := 310*(x[1,1]+x[1,2]+x[1,3])+310*(x[2,1]+x[2,2]+x[2,3])+350*(x[3,1]+x[3,2]+x[3,3])+285*(x[4,1]+x[4,2]+x[4,3]); Balance := [16(x[1,1]+x[2,1]+x[3,1]+x[4,1])-10(x[1,2]+x[2,2]+x[3,2]+x[4,2]), 8(x[1,2]+x[2,2]+x[3,2]+x[4,2])-16(x[1,3]+x[2,3]+x[3,3]+x[4,3])]; Available := [x[1,1]+x[1,2]+x[1,3]-18, x[2,1]+x[2,2]+x[2,3]-15, x[3,1]+x[3,2]+x[3,3]-23, x[4,1]+x[4,2]+x[4,3]-12]; Weight := [x[1,1]+x[2,1]+x[3,1]+x[4,1]-10, x[1,2]+x[2,2]+x[3,2]+x[4,2]-16, x[1,3]+x[2,3]+x[3,3]+x[4,3]-8]; Volume := [480x[1,1]+650x[2,1]+580x[3,1]+390x[4,1]-6800, 480x[1,2]+650x[2,2]+580x[3,2]+390x[4,2]-8700, 480x[1,3]+650x[2,3]+580x[3,3]+390x[4,3]-5300]; LessEq := Flatten([Available, Weight, Volume]); Bounds := [[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""]]; IntNum:=[x[1,2], x[1,3]]; $GLPK.MIPSolve(Objective, Balance, LessEq, [], Bounds, IntNum, [], "Max"); And we receive [x[1,1], x[1,2] - 8, x[1,3], x[2,1], x[2,2] - 3, x[2,3], x[3,1] - 10, x[3,2] - 5, x[3,3] - 8, x[4,1], x[4,2], x[4,3]] This means * in the front we put - 0 of cargo one (x[1,1] = 0) - 0 of cargo two (x[2,1] = 0) - 10 tons of cargo three (x[3,1] = 10) - 0 of cargo four (x[4,1] = 0) * in the middle we put - 8 tons of cargo one (x[1,2] = 8) - 3 of cargo two (x[2,2] = 3) - 5 tons of cargo three (x[3,2] = 5) - 0 of cargo four (x[4,2] = 0) * in the rear we put - 0 tons of cargo one (x[1,3] = 0) - 0 of cargo two (x[2,3] = 0) - 8 tons of cargo three (x[3,3] = 8) - 0 of cargo four (x[4,3] = 0)