ApCoCoA-1:Fundamentals Tutorial De Types: Difference between revisions
No edit summary |
No edit summary |
||
| Line 16: | Line 16: | ||
Also ist <tt>MeineZahl</tt> vom Wert <tt>INT</tt>, also eine ganze Zahl, was bei 5 auch durchaus ersichtlich ist. Die folgende Liste umfasst die häufigsten Objekt-Typen in CoCoA. | Also ist <tt>MeineZahl</tt> vom Wert <tt>INT</tt>, also eine ganze Zahl, was bei 5 auch durchaus ersichtlich ist. Die folgende Liste umfasst die häufigsten Objekt-Typen in CoCoA. | ||
<tt>INT</tt>: Die | |||
<tt>INT</tt>: Die '''ganzen Zahlen''' <math>\mathbb{Z}</math>, also z.B. die Mersensche | |||
Zahl <math>2^{32\,582\,657}-1</math>, eine Zahl mit 9808358 Stellen, welche zugleich auch die | Zahl <math>2^{32\,582\,657}-1</math>, eine Zahl mit 9808358 Stellen, welche zugleich auch die | ||
größte bekannte Primzahl ist. Speichert man diese Zahl in einer Text-Datei ab, so hat diese alleine 9,4MB. | größte bekannte Primzahl ist. Speichert man diese Zahl in einer Text-Datei ab, so hat diese alleine 9,4MB. | ||
| Line 23: | Line 24: | ||
bzw. auf 64-Bit-Computer <math>2^{64}-1=18446744073709551615</math>. | bzw. auf 64-Bit-Computer <math>2^{64}-1=18446744073709551615</math>. | ||
---- | |||
wirklich zwei ganze Zahlen, die geteilt und gekürzt werden. Für | |||
etwas völlig anderes als | <tt>RAT</tt>: '''Rationale Zahlen''' $\mathbb{Q}$. In CoCoA sind dies | ||
wirklich zwei ganze Zahlen, die geteilt und gekürzt werden. Für CoCoA ist <math>\frac{1}{3}</math> | |||
etwas völlig anderes als <math>0,333333333333</math> (<math>=\frac{333333333333}{1000000000000}</math>). | |||
CoCoA kann nicht in <math>\mathbb{R}</math> rechnen, wie denn auch, um z.B. <math>\pi</math> einzulesen (eine | |||
transzendente Zahl, also eine Zahl, mit unendlich vielen Nachkommastellen) müsste man, | transzendente Zahl, also eine Zahl, mit unendlich vielen Nachkommastellen) müsste man, | ||
auch mit noch so schnellen Computern) unendlich lange warten. Aber so schlimm ist das | auch mit noch so schnellen Computern) unendlich lange warten. Aber so schlimm ist das | ||
Ganze ja nun auch wieder nicht Zum einen kann | Ganze ja nun auch wieder nicht Zum einen kann CoCoA symbolisch mit dem Objekt | ||
<math>\pi</math> hervorragend umgehen und zum anderen liegt <math>\mathbb{Q}</math> dicht in <math>\mathbb{R}</math>. | |||
Das bedeutet für uns, dass wir beliebig nahe mit einer rationalen Zahl an eine | Das bedeutet für uns, dass wir beliebig nahe mit einer rationalen Zahl an eine | ||
reelle Zahl herankommen können. So hat schon Archimedes von Syrakus (282 | reelle Zahl herankommen können. So hat schon Archimedes von Syrakus (282-212 v. Chr.), | ||
durch die Betrachtung des regelmäßigen | durch die Betrachtung des regelmäßigen 96-Ecks, <math>\pi</math> wie folgt angenähert: | ||
<center><math>3,14084507042\dots\ =\ 3\frac{10}{71} \ <\ \pi\ <\ 3\frac{1}{7}\ = \ 3,14285714286\dots</math></center> | |||
---- | |||
<tt>LIST</tt>: '''Listen''', sind eine der mächtigsten Konstruktionen in | |||
z.B. | CoCoA. Eine Liste wird immer mit eckigen Klammern beschrieben. So erzeugt | ||
der Zahlen 1 bis 10 enthält, also | z.B. <tt>M:=[1..10];</tt> in CoCoA eine Liste vom Namen <tt>M</tt>, welche die Liste | ||
der Zahlen 1 bis 10 enthält, also <tt>[ [1,2,3,4,5,6,7,8,9,10] ]</tt>. Aber eigentlich wollten | |||
wir doch nur eine Liste der Zahlen 1 bis 10 erzeugen, wir können dazu einfach den | wir doch nur eine Liste der Zahlen 1 bis 10 erzeugen, wir können dazu einfach den | ||
Befehl | Befehl <tt>Flatten(M);</tt> ausführen, dieser vereinfacht die Liste <tt>M</tt> und wir erhalten | ||
nun | nun <tt>[1,2,3,4,5,6,7,8,9,10]</tt>. Dies hätten wir aber auch direkt durch <tt>M:=1..10;</tt> | ||
erhalten. | erhalten. | ||
Listenkonstruktionen sind in {\CoCoA} so wichtig und nützlich, dass ihnen eine eigene Seite | Listenkonstruktionen sind in {\CoCoA} so wichtig und nützlich, dass ihnen eine eigene Seite | ||
gewidmet wird, siehe | gewidmet wird, siehe [[ApCoCoA:Exampels_Tutorial_De_List|Die List mit den Listen]]. | ||
Modulo-Zahlen werden mit | ---- | ||
so liefert die Eingabe | |||
die Anweisung | <tt>ZMOD</tt>: CoCoA kann auch direkt '''modulo''' rechnen. | ||
Modulo-Zahlen werden mit <tt>n%p</tt>, also <math>n\mbox{ mod }p</math> ein- und ausgegeben, | |||
so liefert die Eingabe <tt>4%7 + 5%7;</tt> die Antwort <tt>2%7</tt>. Wohingegen | |||
die Anweisung <tt>4%7 * 5;</tt> die Antwort <tt>-1%7</tt> liefert. CoCoA rechnet also | |||
automatisch weiter modulo, sobald eine modulo-Zahl dabei ist. | automatisch weiter modulo, sobald eine modulo-Zahl dabei ist. | ||
Anführungsstrichen) einfach als | ---- | ||
<tt>STRING</tt>: Eine '''Texteingabe''', hierbei wird die Eingabe (in | |||
Anführungsstrichen) einfach als '''Zeichenfolge''' ohne Bedeutung behandelt. Dieser | |||
Datentyp ist für Fehlermeldungen oder Ausgaben sehr wichtig, so verursacht z.B. | Datentyp ist für Fehlermeldungen oder Ausgaben sehr wichtig, so verursacht z.B. | ||
<tt>Print "Dies ist ein Text!";</tt> die Ausgabe <tt>Dies ist ein Text!</tt>. | |||
unumgänglich, es gibt nur | ---- | ||
<tt>BOOL</tt>: Die '''Boolschen''' Werte sind beim Vergleich von Elementen | |||
unumgänglich, es gibt nur <tt>TRUE</tt> und <tt>FALSE</tt>. So liefert etwa die Anfrage | |||
<tt>1=0;</tt> im Allgemeinen die Ausgabe <tt>FALSE</tt>, wohingegen <tt>1%2=-1%2;</tt> | |||
<tt>TRUE</tt> liefert. | |||
---- | |||
<tt>MAT</tt>: Der Datentyp '''Matrix''': Eine Matrix ist einfach betrachtet eine Liste von | |||
Listen, wobei die Teillisten alle gleich lang sind, d.h. man gibt jede Zeile einer Matrix als | Listen, wobei die Teillisten alle gleich lang sind, d.h. man gibt jede Zeile einer Matrix als | ||
Liste (innerhalb einer Liste) ein. Wichtig ist nun, dass man | Liste (innerhalb einer Liste) ein. Wichtig ist nun, dass man CoCoA sagt, dass es sich um | ||
eine Matrix handelt. So erzeugt | eine Matrix handelt. So erzeugt <tt>L:=[ [2,4],[1,7] ];</tt> die Liste der beiden Listen <tt>[2,4]</tt> | ||
und | und <tt>[1,7]</tt>, wohingegen <tt>M:=Mat([ [2,4],[1,7] ]);</tt> eine Matrix mit den beiden Zeilen <tt>[2,4]</tt> und <tt>[1,7]</tt> erzeugt. Mit <tt>Mat(...);</tt> kann man aus jeder Liste (sofern | ||
ihre Proportionen stimmen) eine Matrix machen und mit <tt>List(...);</tt> kann man aus einer | |||
ihre Proportionen stimmen) eine Matrix machen und mit | |||
Matrix wieder eine Liste von Listen machen. | Matrix wieder eine Liste von Listen machen. | ||
<center> | |||
[[Image:bsp_mat.png]] | |||
</center> | |||
eingegeben, wie man es normalerweise schreibt; so wird das Polynom | ---- | ||
mit | |||
<tt>POLY</tt>: Ein '''Polynom''' in CoCoA wird im Prinzip genau so | |||
eingegeben, wie man es normalerweise schreibt; so wird das Polynom <math>3x^2-y+z-5</math> | |||
mit <tt>P:=3x^ 2-y+z-5;</tt> eingegeben. Exponenten werden mit der | |||
^-Taste eingegeben. Unbestimmte in CoCoA sind die einzigen | |||
Elemente, welche klein geschrieben werden. Man kann immer nur die Unbestimmten | Elemente, welche klein geschrieben werden. Man kann immer nur die Unbestimmten | ||
verwenden, die im (aktuellen) Polynomring vordefiniert sind. | verwenden, die im (aktuellen) Polynomring vordefiniert sind. | ||
Standardmäßig benutzt | Standardmäßig benutzt | ||
CoCoA zu Beginn immer <tt>Q[x,y,z]</tt>, wenn wir mit mehr Variablen rechnen wollen, | |||
so brauchen wir einen größeren Ring, z.B. den Ring | so brauchen wir einen größeren Ring, z.B. den Ring <tt>Q[x[1..10]]</tt>, dieser stellt uns | ||
die Variablen | die Variablen <tt>x[1]</tt> bis <tt>x[10]</tt> zur Verfügung. | ||
---- | |||
Für uns ist vor allem die erste Eigenschaft wichtig. So ist | |||
Vielfachen von | <tt>IDEAL</tt>: Ein Ideal des Polynomrings <math>R</math> ist die Teilmenge <math>I</math>, für die gilt | ||
<math>R\cdot I\subseteq I</math> und dass <math>\left(I,+\right)</math> eine Untergruppe von <math>\left(R,+\right)</math> ist. | |||
So ist dann das Ideal von | Für uns ist vor allem die erste Eigenschaft wichtig. So ist <tt>Ideal(x);</tt>, die Menge aller | ||
wobei die | Vielfachen von <tt>x</tt>, bzw. aller Polynome, die <tt>x</tt> enthalten, d.h. das Polynom | ||
<tt>y</tt> ist nicht in <tt>Ideal(x)</tt>. | |||
nur dass die Elemente in der | |||
gewohnten Vektoren wie z.B. | So ist dann das Ideal von <math>f_1,\ldots,f_n</math> die Menge aller Polynome <math>f_1g_1+\ldots+f_ng_n</math>, | ||
wobei die <math>g_i</math> beliebige Polynome aus unserem Polynomring sind. | |||
---- | |||
<tt>VECTOR</tt>: Ein '''Vector''' ist der gewohnte Vektor, also eine 1xn-Matrix, | |||
nur dass die Elemente in der CoCoA-Version des Vektors Polynome sind. Dies lässt natürlich die | |||
gewohnten Vektoren wie z.B. <math>\left(1,3,6\right)</math> zu. | |||
Revision as of 17:58, 15 July 2008
Zahlen, Vektoren, Matrizen oder einfach nur Listen?
CoCoA stellt verschiedene Objekttypen zur Verfügung, aber eh wir uns diese genauer anschauen, müssen wir erst etwas über Zuweisungen und neue Objekte in Erfahrung bringen.
Wie die CoCoA-Befehle, so beginnen auch die Objekte in CoCoA mit einem Großbuchstaben. Die einzigen Objekte, welche klein geschrieben werden sind Variablen, d.h. aber auch, dass CoCoA zum Beispiel quit; als das Produkt betrachtet. Dies ist eine beliebte Fehlerquelle. \medskip
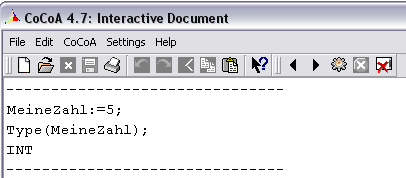
Wollen wir z.B. dem Objekt MeineZahl den Wert 5 zuweisen, so schreiben wir MeineZahl:=5;. CoCoA legt also ein neues Objekt (MeineZahl) an und weist ihm den Wert 5 zu. Zuweisungen werden mit := gemacht und natürlich mit einem Semikolon abgeschlossen. \medskip
Aber was ist 5 nun für ein Objekt-Typ? Dies lässt sich mit dem Befehl Type(...); herausfinden.
Also ist MeineZahl vom Wert INT, also eine ganze Zahl, was bei 5 auch durchaus ersichtlich ist. Die folgende Liste umfasst die häufigsten Objekt-Typen in CoCoA.
INT: Die ganzen Zahlen , also z.B. die Mersensche
Zahl , eine Zahl mit 9808358 Stellen, welche zugleich auch die
größte bekannte Primzahl ist. Speichert man diese Zahl in einer Text-Datei ab, so hat diese alleine 9,4MB.
Hingegen ist die größte ganze Zahl, die auf einem
32-Bit-Computer üblicherweise verwendet werden kann ,
bzw. auf 64-Bit-Computer .
RAT: Rationale Zahlen $\mathbb{Q}$. In CoCoA sind dies wirklich zwei ganze Zahlen, die geteilt und gekürzt werden. Für CoCoA ist etwas völlig anderes als (). CoCoA kann nicht in rechnen, wie denn auch, um z.B. einzulesen (eine transzendente Zahl, also eine Zahl, mit unendlich vielen Nachkommastellen) müsste man, auch mit noch so schnellen Computern) unendlich lange warten. Aber so schlimm ist das Ganze ja nun auch wieder nicht Zum einen kann CoCoA symbolisch mit dem Objekt hervorragend umgehen und zum anderen liegt dicht in . Das bedeutet für uns, dass wir beliebig nahe mit einer rationalen Zahl an eine reelle Zahl herankommen können. So hat schon Archimedes von Syrakus (282-212 v. Chr.), durch die Betrachtung des regelmäßigen 96-Ecks, wie folgt angenähert:
LIST: Listen, sind eine der mächtigsten Konstruktionen in CoCoA. Eine Liste wird immer mit eckigen Klammern beschrieben. So erzeugt z.B. M:=[1..10]; in CoCoA eine Liste vom Namen M, welche die Liste der Zahlen 1 bis 10 enthält, also [ [1,2,3,4,5,6,7,8,9,10] ]. Aber eigentlich wollten wir doch nur eine Liste der Zahlen 1 bis 10 erzeugen, wir können dazu einfach den Befehl Flatten(M); ausführen, dieser vereinfacht die Liste M und wir erhalten nun [1,2,3,4,5,6,7,8,9,10]. Dies hätten wir aber auch direkt durch M:=1..10; erhalten.
Listenkonstruktionen sind in {\CoCoA} so wichtig und nützlich, dass ihnen eine eigene Seite gewidmet wird, siehe Die List mit den Listen.
ZMOD: CoCoA kann auch direkt modulo rechnen. Modulo-Zahlen werden mit n%p, also ein- und ausgegeben, so liefert die Eingabe 4%7 + 5%7; die Antwort 2%7. Wohingegen die Anweisung 4%7 * 5; die Antwort -1%7 liefert. CoCoA rechnet also automatisch weiter modulo, sobald eine modulo-Zahl dabei ist.
STRING: Eine Texteingabe, hierbei wird die Eingabe (in Anführungsstrichen) einfach als Zeichenfolge ohne Bedeutung behandelt. Dieser Datentyp ist für Fehlermeldungen oder Ausgaben sehr wichtig, so verursacht z.B. Print "Dies ist ein Text!"; die Ausgabe Dies ist ein Text!.
BOOL: Die Boolschen Werte sind beim Vergleich von Elementen unumgänglich, es gibt nur TRUE und FALSE. So liefert etwa die Anfrage 1=0; im Allgemeinen die Ausgabe FALSE, wohingegen 1%2=-1%2; TRUE liefert.
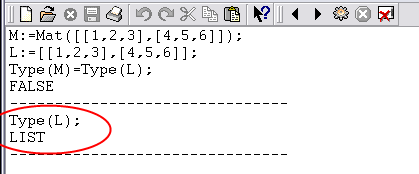
MAT: Der Datentyp Matrix: Eine Matrix ist einfach betrachtet eine Liste von Listen, wobei die Teillisten alle gleich lang sind, d.h. man gibt jede Zeile einer Matrix als Liste (innerhalb einer Liste) ein. Wichtig ist nun, dass man CoCoA sagt, dass es sich um eine Matrix handelt. So erzeugt L:=[ [2,4],[1,7] ]; die Liste der beiden Listen [2,4] und [1,7], wohingegen M:=Mat([ [2,4],[1,7] ]); eine Matrix mit den beiden Zeilen [2,4] und [1,7] erzeugt. Mit Mat(...); kann man aus jeder Liste (sofern ihre Proportionen stimmen) eine Matrix machen und mit List(...); kann man aus einer Matrix wieder eine Liste von Listen machen.
POLY: Ein Polynom in CoCoA wird im Prinzip genau so eingegeben, wie man es normalerweise schreibt; so wird das Polynom mit P:=3x^ 2-y+z-5; eingegeben. Exponenten werden mit der ^-Taste eingegeben. Unbestimmte in CoCoA sind die einzigen Elemente, welche klein geschrieben werden. Man kann immer nur die Unbestimmten verwenden, die im (aktuellen) Polynomring vordefiniert sind. Standardmäßig benutzt CoCoA zu Beginn immer Q[x,y,z], wenn wir mit mehr Variablen rechnen wollen, so brauchen wir einen größeren Ring, z.B. den Ring Q[x[1..10]], dieser stellt uns die Variablen x[1] bis x[10] zur Verfügung.
IDEAL: Ein Ideal des Polynomrings ist die Teilmenge , für die gilt und dass eine Untergruppe von ist. Für uns ist vor allem die erste Eigenschaft wichtig. So ist Ideal(x);, die Menge aller Vielfachen von x, bzw. aller Polynome, die x enthalten, d.h. das Polynom y ist nicht in Ideal(x).
So ist dann das Ideal von die Menge aller Polynome , wobei die beliebige Polynome aus unserem Polynomring sind.
VECTOR: Ein Vector ist der gewohnte Vektor, also eine 1xn-Matrix, nur dass die Elemente in der CoCoA-Version des Vektors Polynome sind. Dies lässt natürlich die gewohnten Vektoren wie z.B. zu.