ApCoCoA-1:Examples Tutorial De Logic
Etwas Aussagen-Logik
In der Logik ist man auf der Suche nach Wahrheitswerten von Formeln. Logische Formel können entweder "wahr" (Wahrheitswert 1) oder "falsch" (Wahrheitswert 0) sein. Die Suche nach den Wahrheitswerten einer Formel verwandeln wir, wie schon bei der Suche nach den Lösungen eines linearen Gleichungssystems (siehe Kapitel Lineare Gleichungssysteme), in die Suche nach Nullstellen. Dies bedeute für uns, dass wir die logischen Formeln in Polynome über dem Körper , welcher nur aus den Elementen 0 und 1 besteht, übersetzen müssen.
Zuallererst müssen wir festlegen, wie wir Texte in aussagenlogische Formeln übersetzen. Dafür brauchen wir zunächst mal Abkürzungen (hier und ), welche für eine Aussage stehen, die entweder wahr oder falsch sein kann.

Diese Übersetzungen haben dann, abhängig von den Wahrheitswerten von und , die folgenden Wahrheitswerte.
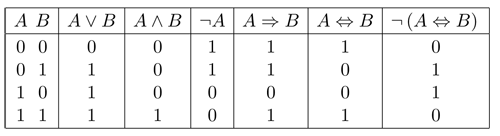
Diese logischen Formeln übersetzen wir jetzt in Polynome über , so dass die Belegung "Wahrheitswert 1" in die "Nullstelle 1" übersetzt wird.

So gilt z.B. für die folgenden Kombinationen von und : , und . Dies sind genau die gleichen Werte, bei denen den Wahrheitswert 1 hat (, und ).
Die ganze Sache funktioniert natürlich nur dann, wenn man für und nicht nur Elementarereignisse einsetzen kann, sondern auch schon erzeugte logische Formeln/Polynome. Die Übersetzungsregeln ändern sich nur geringfügig, vorausgesetzt wir haben bereits mit den obigen Regeln die Formeln und in die Polynome und übersetzt.
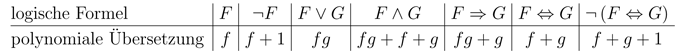
Setzen wir für die Übersetzung von , also , und für die Übersetzung von , also , ein, so erhalten wir über die obige Tabelle zurück. Hierbei ist zu beachten, dass im Polynomring gilt, also gilt auch unabhängig von .
Beispiel
In einer Firma werden zur Zeit die drei Projekte $A$, $B$ und $C$ bearbeitet. Um herauszufinden, welche Projekte bis zum Ende der Woche abgeschlossen werden, befragt der Chef der Firma die jeweiligen Projektleiter und erh\"alt folgende Angaben: \begin{enumerate}\renewcommand{\labelenumi}{\arabic{enumi})}\addtolength{\itemsep}{-0.5em} \item Es k\"onnen nicht alle Projekte fertiggestellt werden. \item Um Projekt $B$ fertigstellen zu k\"onnen, muss Projekt $A$ fertiggestellt sein. \item Es wird auf jeden Fall Projekt $B$ oder Projekt $C$ fertiggestellt. \item Projekt $C$ kann nur fertiggestellt werden, wenn Projekt $B$ fertiggestellt ist. \end{enumerate} Bestimmen Sie diejenigen Projekte, die bis zum Ende der Woche fertiggestellt werden.
Lösung mit CoCoA
\begin{itemize} \item Festlegung der Abk\"urzungen: \begin{center} $\begin{array}{rcccl} A & = & \text{{\glqq}Projekt $A$ wird bis Ende der Woche fertig{\grqq}} & = & a+1, \\ B & = & \text{{\glqq}Projekt $B$ wird bis Ende der Woche fertig{\grqq}} & = & b+1, \\ C & = & \text{{\glqq}Projekt $C$ wird bis Ende der Woche fertig{\grqq}} & = & c+1. \end{array}$ \end{center} \item \"Ubersetzung der Aussagen: \begin{itemize} \item {\glqq}Es k\"onnen nicht alle Projekte fertiggestellt werden{\grqq}: \begin{equation*} F_1 \ :=\ \neg\left(A\wedge B\wedge C\right). \end{equation*} Zuerst übersetzten wir $\left(A\wedge B\right)$ mittels der ersten Tabelle zu $ab+1=:f$ und $C$ zu $c+1=:g$, damit wird dann (siehe zweite Tabelle) $\left(\left(A\wedge B\right)\wedge C\right)$ zu $\left(ab+1\right)\left(c+1\right)+\left(ab+1\right)+\left(c+1\right)= abc + 1$. Jetzt fehlt nur noch das $\neg$ in der Übersetzung, also lautet das zugehölrige Polynom \begin{equation*} f_1=abc. \end{equation*} \item {\glqq}Um Projekt $B$ fertigstellen zu k\"onnen, muss Projekt $A$ fertiggestellt sein{\grqq}: \begin{equation*} F_2\ :=\ \left(B\Rightarrow A\right), \end{equation*} mit dem zugehörigen Polynom \begin{equation*} f_2=ba+b. \end{equation*} \item {\glqq}Es wird auf jeden Fall Projekt $B$ oder Projekt $C$ fertiggestellt{\grqq}: \begin{equation*} F_3\ :=\ \left(B\vee C\right), \end{equation*} das zugehörige Polynom lautet \begin{equation*} f_3=bc+b+c+1. \end{equation*} \item {\glqq}Projekt $C$ kann nur fertiggestellt werden, wenn Projekt $B$ fertiggestellt ist{\grqq}: \begin{equation*} F_4\ :=\ \left(C\Rightarrow B\right), \end{equation*} und \begin{equation*} f_4=cb+c. \end{equation*} \end{itemize} \item {\CoCoA}\smallskip\\ Zuerst müssen wir in {\CoCoA} den passenden Ring eingeben \begin{center} \ttfamily Use S::=Z/(2)[a,b,c]; \end{center} Dann brauchen wir noch das Körperideal, welches die Nullstellen auf $0$ und $1$ festlegt \begin{center} \ttfamily K:=Ideal(a\textasciicircum 2+a, b\textasciicircum 2+b, c\textasciicircum 2+c); \end{center} Als nächstes geben wir die übersetzten Polynome ein \begin{center} \ttfamily I:=Ideal(abc, ba+b, bc+b+c+1, cb+c) + K; \end{center} und erhalten mittels \begin{center} \ttfamily ReducedGBasis(I); \end{center} die Antwort \begin{center} {\ttfamily [b+1, a+1, c]}. \end{center} \item Also müssen der Wahrheitswert von $A$, die Nullstelle von $a+1$, und der Wahrheitswert von $B$, die Nullstelle von $b+1$, $1$ sein und der Wahrheitswert von $C$, die Nullstelle von $c$, $0$. Also werden die Projekte $A$ und $B$ bis Ende der Woche fertig. \end{itemize}
Weiter geht's im Kapitel Ein rundes Beispiel.



















![{\displaystyle \mathbb {F} _{2}\left[x,y\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/139eed9a79db55789822d5b64bb4e5798d509f74)

