ApCoCoA-1:Examples Tutorial De Equation
Lineare Gleichungssysteme
Mit CoCoA ist es ein leichtes, Gleichungssysteme zu lösen, wir müssen sie nur ein wenig umformulieren. Wir müssen lediglich die Suche nach der Lösung des Systems in eine Suche nach gemeinsamen Nullstellen verwandeln. Dafür schreiben wir für jede Gleichung die äquivalente Form . Die Suche nach gemeinsamen Nullstellen ist die Suche nach einer Gröbner-Basis eines Ideals. Hierbei liefert uns die Idealschreibweise, die Suche nach den gemeinsamen Lösungen und die Suche nach einer (Gröbner-)Basis die Lösung für all diese Polynome. Wir brauchen dann nur das Ergebnis wieder in Gleichungen zurück zu übersetzen.
Betrachten wir das folgende Gleichungssystem:
Umgeschrieben in eine Nullstellensuche sieht das System jetzt so aus:
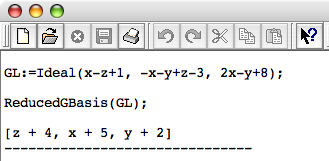
In CoCoA geben wir das Ideal mit dem Ideal(...);-Befehl ein, also
Gl:=Ideal(x-z+1, -x-y+z-3, 2x-y+8);
Jetzt berechnen wir die Reduzierte Gröbner-Basis diese Ideals
ReducedGBasis(Gl);
und erhalten
[z + 4, x + 5, y + 2].
Also gilt , und .
Weiter geht's im Kapitel Euklidischer Algorithmus.










