ApCoCoA-1:MatlabToolbox

Introduction

The MatlabToolbox is a collection of .m and .mex files to use the functions provided by the ApCoCoALib. Classes representing rings, polynomials, ideals and modules are added to provide an intuitive approach to the algebraic nature of the functions.

To overcome technical difficulties the interaction with the ApCoCoALib is done via a dll. For more technical details how this dll is programmed have a look at the MatlabToolbox Interface.

The MatlabToolbox in it's current state needs to be compiled by the user on Windows with MSVC. Read the howto page for a description of the compilation process: HowTo: Compile MatlabToolbox on Windows

Note: From a perspective of an ApCoCoA User this toolbox provides an interface to communicate with Matlab - thus the toolbox is called in this Wiki MatlabToolbox. Yet from the perspective of a Matlab user the toolbox provides an interface to communicate with the ApCoCoALib - thus the compiled library is called ApCoCoAToolbox.dll.

MatlabToolbox structure

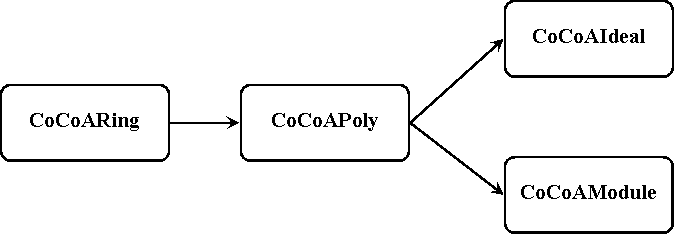
The toolbox is based on classes to handle multivariate polynomials. The concept is based on a ring representing class called CoCoARing. Then a multivariate polynomial is build with coefficients defined over a CoCoARing. The polynomial is an element of the CoCoAPoly class.

Multiple CoCoAPoly's can be combined in an array. In many cases a list of polynomials (a 1xN array) is interpreted as the set of generators of an ideal. To represent this view and provide common operations on ideals the class CoCoAIdeal is introduced.

A MxN array of CoCoAPoly's could then be interpreted as a set of generators for a module and the class CoCoAModule is introduced to provide common module operations.

Figure 1: Class structure

Note: Due to technical limitations the current implementation assumes that all polynomials are defined over the ring Q[x1,...xn]. General ring support in the CoCoAPoly class will be added in a later stage.

The structure of the MatlabToolbox is depicted in figure 1.

Detailed descriptions for each class and its methods are given at the following links:

• CoCoARing
• CoCoAPoly
• CoCoAIdeal
• CoCoAModule

Available functions

The interface provides mex functions to call the ApCoCoALib functions. These functions are located in the subfolder MexFiles.

But the mex files parameters for polynomial operations are based on double matrices representing the polynomials. This syntax is far away from an intuitive handling of polynomials. Thus wrapper functions have been written to provide automated conversion from CoCoAPoly's, CoCoAIdeal's or CoCoAModule's.

For example to compute the Groebner Basis of an ideal one can call the function GBasisIdeal_wrap(InputIdeal) which takes a CoCoAIdeal, computes the Groebner Basis and returns the result as a CoCoAPoly list. To store the Groebner Basis in the ideal the ideal method computeGBasis(InputIdeal) can be used. This functions also computes the Groebner Basis but adds the result to the ideals attribute GBasis.

The wrapper files are bundled in a subfolder called MatlabFiles. The filename is indicating which type of input is needed. E.g. GBasisModule_wrap() takes a CoCoAModule and returns the Groebner Basis as a list of CoCoAPoly's.

The mex files and if available the corresponding wrapper files are individually described at the following links. In case that there are versions available for ideals and modules these functions are described on the same page. Note that some of the mex files are used to define methods for the described classes and that there is no corresponding wrapper file available.

• APVI: Computes the approximate vanishing ideal of a set of points.
• CColon: Computes ... for the given ideal or module.
• CoCoAPolyPower: Computes ... for the given polynomial.
• Colon: Computes ... for the given ideal or module.
• GBasis: Computes ... for the given ideal or module.
• Intersection: Computes ... for the given ideal or module.
• PolyRingHom: Applies a ring homomorphism to the given polynmonial.
• Preprocess: Algebraic preprocessing of multi dimensional points.
• SATGBasis: Computes ... for the given ideal or module.
• SATMixGBasis: Computes ... for the given ideal or module.
• Saturation: Computes ... for the given ideal or module.
• SSaturation: Computes ... for the given ideal or module.
• Syzygy: Computes ... for the given ideal or module.