ApCoCoA-1:GLPK.MIPSolve

LPSolve

solve linear programms

Syntax

GLPK.MIPSolve(Objective_f:POLYNOM, EQ_Poly:LIST, LE_Poly:LIST, GE_Poly:LIST, Bounds:LIST, IntNum:LIST, Binaries:LIST, MinMax:STRING)

Description

Please note: The function(s) explained on this page is/are using the ApCoCoAServer. You will have to start the ApCoCoAServer in order to use

it/them.

Objective_f: A linear polynomial which is equivalent to the linear objective function.

EQ_Poly: List of linear polynomials, which are equivalent to the equality-part in the list of conditions.

LE_Poly: List of linear polynomials, which are equivalent to the lower or equal-part in the list of conditions.

GE_Poly: List of linear polynomials, which are equivalent to the greater or equal-part in the list of conditions.

Bounds: List of lists with two elements. Each List contains the lower and upper bounds for each variable. You can choose between INT or RAT for the type of each bound, if you type in a (empty) string, then it means minus infinity (first place) or plus infinity (second place).

IntNum: List of variables, which should be integer. Note: For each variable in this list, the borders get rounded (lower bound: up and upper bound: down). In the case that the lower rounded bound becomes greater then the upper rounded bound, glpk returns: Solution Status: INTEGER UNDEFINED - Value of objective function: 0.

Binaries: List of variables, which should be binaries (0 or 1).

MinMax: Minimization ("Min") or maximization ("Max"), that's the question.

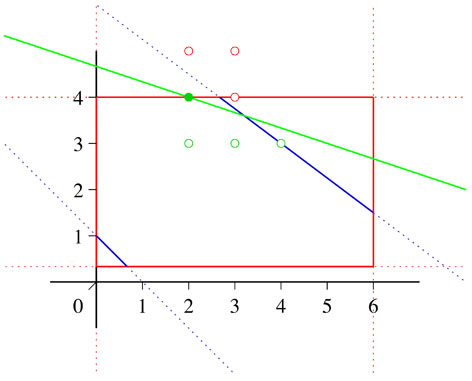
First we want to discuss a rather easy example.

Example

We want to maximize the Function y = - 1/2x, 
with the two conditions y ≤ 6 - 3/4x and y ≥ 1 - x and the bounds 0 ≤ x ≤ 6 and 1/3 ≤ y ≤ 4.

We prename the input of GLPK.MIPSolve-function.
Use S::=Q[x,y];
OF := 1/2x + y;
LE := [3/4x + y - 6];
GE := [x + y - 1];
Bounds:=[[0,6], [1/3,4]];
IntNum:=[x,y];

Then we compute the solution with
$GLPK.MIPSolve(OF, [], LE, GE, Bounds, IntNum, [], "Max");


And we achieve:
Solution Status: INTEGER OPTIMAL
Value of objective function: 5
[x[1] - 2, x[2] - 4]

Example

''Linear programming example 1996 MBA exam''

A cargo plane has three compartments for storing cargo: front, centre and rear. 
These compartments have the following limits on both weight and space:

Compartment   Weight capacity (tonnes)   Space capacity (cubic metres)
Front         10                         6800
Centre        16                         8700
Rear          8                          5300

Furthermore, the weight of the cargo in the respective compartments must be the same 
proportion of that compartment's weight capacity to maintain the balance of the plane.

The following four cargoes are available for shipment on the next flight:

Cargo   Weight (tonnes)   Volume (cubic metres/tonne)  Profit (£/tonne)
C1      18                480                          310
C2      15                650                          380
C3      23                580                          350
C4      12                390                          285

Any proportion of these cargoes can be accepted. The objective is to determine how much 
(if any) of each cargo C1, C2, C3 and C4 should be accepted and how to distribute each 
among the compartments so that the total profit for the flight is maximised. 


To solve this problem we had to compose a linear program.

Variables

We need to decide how much of each of the four cargoes to put in each of the three compartments. 
Hence let:

xij be the number of tonnes of cargo i (i=1,2,3,4 for C1, C2, C3 and C4 respectively) that is put into 
compartment j (j=1 for Front, j=2 for Centre and j=3 for Rear) where xij >=0 i=1,2,3,4; j=1,2,3

Note here that we are explicitly told we can split the cargoes into any proportions (fractions) that we like.

Constraints

* cannot pack more of each of the four cargoes than we have available

x11 + x12 + x13 ≤ 18
x21 + x22 + x23 ≤ 15
x31 + x32 + x33 ≤ 23
x41 + x42 + x43 ≤ 12

* the weight capacity of each compartment must be respected

x11 + x21 + x31 + x41 ≤ 10
x12 + x22 + x32 + x42 ≤ 16
x13 + x23 + x33 + x43 ≤ 8

* the volume (space) capacity of each compartment must be respected

480x11 + 650x21 + 580x31 + 390x41 ≤ 6800
480x12 + 650x22 + 580x32 + 390x42 ≤ 8700
480x13 + 650x23 + 580x33 + 390x43 ≤ 5300

* the weight of the cargo in the respective compartments must be the same proportion 
  of that compartment's weight capacity to maintain the balance of the plane

[x11 + x21 + x31 + x41]/10 = [x12 + x22 + x32 + x42]/16 = [x13 + x23 + x33 + x43]/8

Objective

The objective is to maximise total profit, i.e.

maximise 310[x11+ x12+x13] + 380[x21+ x22+x23] + 350[x31+ x32+x33] + 285[x41+ x42+x43]

The basic assumptions are:

* that each cargo can be split into whatever proportions/fractions we desire
* that each cargo can be split between two or more compartments if we so desire
* that the cargo can be packed into each compartment (for example if the cargo was spherical it would 
  not be possible to pack a compartment to volume capacity, some free space is inevitable in sphere packing)
* all the data/numbers given are accurate


In ApCoCoa you can solve this LP like this:

Use S::= Q[x[1..4,1..3]];

Objective := 310*(x[1,1]+x[1,2]+x[1,3])+310*(x[2,1]+x[2,2]+x[2,3])+350*(x[3,1]+x[3,2]+x[3,3])+285*(x[4,1]+x[4,2]+x[4,3]);
Balance := [16(x[1,1]+x[2,1]+x[3,1]+x[4,1])-10(x[1,2]+x[2,2]+x[3,2]+x[4,2]), 8(x[1,2]+x[2,2]+x[3,2]+x[4,2])-16(x[1,3]+x[2,3]+x[3,3]+x[4,3])];

Available := [x[1,1]+x[1,2]+x[1,3]-18, x[2,1]+x[2,2]+x[2,3]-15, x[3,1]+x[3,2]+x[3,3]-23, x[4,1]+x[4,2]+x[4,3]-12];
Weight := [x[1,1]+x[2,1]+x[3,1]+x[4,1]-10, x[1,2]+x[2,2]+x[3,2]+x[4,2]-16, x[1,3]+x[2,3]+x[3,3]+x[4,3]-8];
Volume := [480x[1,1]+650x[2,1]+580x[3,1]+390x[4,1]-6800, 480x[1,2]+650x[2,2]+580x[3,2]+390x[4,2]-8700, 480x[1,3]+650x[2,3]+580x[3,3]+390x[4,3]-5300];
LessEq := Flatten([Available, Weight, Volume]);

Bounds := [[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""],[0,""]];

IntNum:=[x[1,2], x[1,3]];

$GLPK.MIPSolve(Objective, Balance, LessEq, [], Bounds, IntNum, [], "Max");


And we receive:
Solution Status: INTEGER OPTIMAL
Value of objective function: 11460
[x[1,1], x[1,2] - 8, x[1,3], x[2,1], x[2,2] - 3, x[2,3], x[3,1] - 10, x[3,2] - 5, x[3,3] - 8, x[4,1], x[4,2], x[4,3]]

This means 
* in the front we put
  - 0 of cargo one (x[1,1] = 0)
  - 0 of cargo two (x[2,1] = 0)
  - 10 tons of cargo three (x[3,1] = 10)
  - 0 of cargo four (x[4,1] = 0)
* in the middle we put
  - 8 tons of cargo one (x[1,2] = 8)
  - 3 of cargo two (x[2,2] = 3)
  - 5 tons of cargo three (x[3,2] = 5)
  - 0 of cargo four (x[4,2] = 0)
* in the rear we put
  - 0 tons of cargo one (x[1,3] = 0)
  - 0 of cargo two (x[2,3] = 0)
  - 8 tons of cargo three (x[3,3] = 8)
  - 0 of cargo four (x[4,3] = 0)