Difference between revisions of "ApCoCoA-1:Heisenberg groups"
From ApCoCoAWiki
| Line 7: | Line 7: | ||
Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by: | Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by: | ||
H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j | H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j | ||
| − | + | ||
| + | ==== Reference ==== | ||
| + | Ernst Binz and Sonja Pods, Geometry of Heisenberg Groups, American Mathematical Society, 2008. | ||
==== Computation ==== | ==== Computation ==== | ||
Revision as of 09:23, 23 August 2013
Description
The Heisenberg group is the group of 3x3 upper triangular matrices of the form
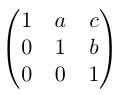
Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by:
H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j
Reference
Ernst Binz and Sonja Pods, Geometry of Heisenberg Groups, American Mathematical Society, 2008.
Computation
/*Use the ApCoCoA package ncpoly.*/
// Number of Heisenberg group
MEMORY.N:=1;
// a invers to d and b invers to e and c invers to f
Use ZZ/(2)[a[1..MEMORY.N],b[1..MEMORY.N],c,d[1..MEMORY.N],e[1..MEMORY.N],f];
NC.SetOrdering("LLEX");
Define CreateRelationsHeisenberg()
Relations:=[];
// add the relations of the invers elements ad = da = be = eb = cf = fc = 1
Append(Relations,[[c,f],[1]]);
Append(Relations,[[f,c],[1]]);
For Index1 := 1 To MEMORY.N Do
Append(Relations,[[a[Index1],d[Index1]],[1]]);
Append(Relations,[[d[Index1],a[Index1]],[1]]);
Append(Relations,[[b[Index1],e[Index1]],[1]]);
Append(Relations,[[e[Index1],b[Index1]],[1]]);
EndFor;
// add the relation [a_{i}, b_{i}] = c
For Index2 := 1 To MEMORY.N Do
Append(Relations,[[a[Index2],b[Index2],d[Index2],e[Index2]],[c]]);
EndFor;
// add the relation [a_{i}, c] = [b_i, c]
For Index3 := 1 To MEMORY.N Do
Append(Relations,[[a[Index3],c,d[Index3],f],[b[Index3],c,e[Index3],f]]);
EndFor;
// add the relation [a_{i}, b_{j}] = 1 for all i != j
For Index4 := 1 To MEMORY.N Do
For Index5 := 1 To MEMORY.N Do
If Index4 <> Index5 Then
Append(Relations,[[a[Index4],b[Index5],d[Index4],e[Index5]],[1]]);
EndIf;
Endfor;
EndFor;
Return Relations;
EndDefine;
Relations:=CreateRelationsHeisenberg();
Relations;
Size(Relations);
GB:=NC.GB(Relations,31,1,100,1000);
Size(GB);