ApCoCoA-1:Heisenberg groups

Heisenberg groups

Description

The Heisenberg group is the group of 3x3 upper triangular matrices of the form

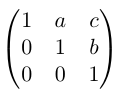
Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by:

 H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j

(Reference: Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical Society)

Computation

 /*Use the ApCoCoA package ncpoly.*/
 
 // Number of Heisenberg group
 MEMORY.N:=1;
 
 // a invers to d and b invers to e and c invers to f
 Use ZZ/(2)[a[1..MEMORY.N],b[1..MEMORY.N],c,d[1..MEMORY.N],e[1..MEMORY.N],f];
 NC.SetOrdering("LLEX");
 Define CreateRelationsHeisenberg()
   Relations:=[];
   // add the relations of the invers elements ad = da = be = eb = cf = fc = 1
   Append(Relations,[[c,f],[1]]);
   Append(Relations,[[f,c],[1]]);
   For Index1 := 1 To MEMORY.N Do
     Append(Relations,[[a[Index1],d[Index1]],[1]]);
     Append(Relations,[[d[Index1],a[Index1]],[1]]);
     Append(Relations,[[b[Index1],e[Index1]],[1]]);
     Append(Relations,[[e[Index1],b[Index1]],[1]]);
   EndFor;
   
   // add the relation [a_{i}, b_{i}] = c
   For Index2 := 1 To MEMORY.N Do
     Append(Relations,[[a[Index2],b[Index2],d[Index2],e[Index2]],[c]]);
   EndFor;
   
   // add the relation [a_{i}, c] = [b_i, c]
   For Index3 := 1 To MEMORY.N Do
     Append(Relations,[[a[Index3],c,d[Index3],f],[b[Index3],c,e[Index3],f]]);
   EndFor;
   
   // add the relation [a_{i}, b_{j}] = 1 for all i != j
   For Index4 := 1 To MEMORY.N Do
     For Index5 := 1 To MEMORY.N Do
       If Index4 <> Index5 Then
         Append(Relations,[[a[Index4],b[Index5],d[Index4],e[Index5]],[1]]);
       EndIf;
     Endfor;
   EndFor;
   
   Return Relations;
 EndDefine;
 
 Relations:=CreateRelationsHeisenberg();
 Relations;
 Size(Relations);
 GB:=NC.GB(Relations,31,1,100,1000);
 Size(GB);