Difference between revisions of "ApCoCoA-1:Heisenberg groups"
From ApCoCoAWiki
StrohmeierB (talk | contribs) |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | === <div id="Heisenberg_groups">[[:ApCoCoA:Symbolic data#Heisenberg_groups|Heisenberg | + | === <div id="Heisenberg_groups">[[:ApCoCoA:Symbolic data#Heisenberg_groups|Heisenberg Groups]]</div> === |
==== Description ==== | ==== Description ==== | ||
The Heisenberg group is the group of 3x3 upper triangular matrices of the form | The Heisenberg group is the group of 3x3 upper triangular matrices of the form | ||
| Line 7: | Line 7: | ||
Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by: | Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by: | ||
H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j | H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j | ||
| − | + | ||
| + | ==== Reference ==== | ||
| + | Ernst Binz and Sonja Pods, Geometry of Heisenberg Groups, American Mathematical Society, 2008. | ||
==== Computation ==== | ==== Computation ==== | ||
| Line 18: | Line 20: | ||
Use ZZ/(2)[a[1..MEMORY.N],b[1..MEMORY.N],c,d[1..MEMORY.N],e[1..MEMORY.N],f]; | Use ZZ/(2)[a[1..MEMORY.N],b[1..MEMORY.N],c,d[1..MEMORY.N],e[1..MEMORY.N],f]; | ||
NC.SetOrdering("LLEX"); | NC.SetOrdering("LLEX"); | ||
| + | |||
Define CreateRelationsHeisenberg() | Define CreateRelationsHeisenberg() | ||
Relations:=[]; | Relations:=[]; | ||
| − | // add the relations of the | + | |
| + | // add the relations of the inverse elements ad = da = be = eb = cf = fc = 1 | ||
Append(Relations,[[c,f],[1]]); | Append(Relations,[[c,f],[1]]); | ||
Append(Relations,[[f,c],[1]]); | Append(Relations,[[f,c],[1]]); | ||
| Line 55: | Line 59: | ||
Relations; | Relations; | ||
Size(Relations); | Size(Relations); | ||
| − | + | ||
| − | Size( | + | Gb:=NC.GB(Relations,31,1,100,1000); |
| + | Size(Gb); | ||
| + | ====Examples in Symbolic Data Format==== | ||
| + | =====Heisenberg group 1===== | ||
| + | <FREEALGEBRA createdAt="2014-03-04" createdBy="strohmeier"> | ||
| + | <vars>a1,b1,c,d1,e1,f</vars> | ||
| + | <uptoDeg>7</uptoDeg> | ||
| + | <basis> | ||
| + | <ncpoly>c*f-1</ncpoly> | ||
| + | <ncpoly>f*c-1</ncpoly> | ||
| + | <ncpoly>a1*d1-1</ncpoly> | ||
| + | <ncpoly>d1*a1-1</ncpoly> | ||
| + | <ncpoly>b1*e1-1</ncpoly> | ||
| + | <ncpoly>e1*b1-1</ncpoly> | ||
| + | <ncpoly>a1*b1*d1*e1-c</ncpoly> | ||
| + | <ncpoly>a1*c*d1*f-b1*c*e1*f</ncpoly> | ||
| + | </basis> | ||
| + | <Comment>Heisenberg_group_1</Comment> | ||
| + | </FREEALGEBRA> | ||
| + | =====Heisenberg group 2===== | ||
| + | <FREEALGEBRA createdAt="2014-03-04" createdBy="strohmeier"> | ||
| + | <vars>a1,a2,b1,b2,c,d1,d2,e1,e2,f</vars> | ||
| + | <uptoDeg>5</uptoDeg> | ||
| + | <basis> | ||
| + | <ncpoly>c*f-1</ncpoly> | ||
| + | <ncpoly>f*c-1</ncpoly> | ||
| + | <ncpoly>a1*d1-1</ncpoly> | ||
| + | <ncpoly>d1*a1-1</ncpoly> | ||
| + | <ncpoly>b1*e1-1</ncpoly> | ||
| + | <ncpoly>e1*b1-1</ncpoly> | ||
| + | <ncpoly>a2*d2-1</ncpoly> | ||
| + | <ncpoly>d2*a2-1</ncpoly> | ||
| + | <ncpoly>b2*e2-1</ncpoly> | ||
| + | <ncpoly>e2*b2-1</ncpoly> | ||
| + | <ncpoly>a1*b1*d1*e1-c</ncpoly> | ||
| + | <ncpoly>a2*b2*d2*e2-c</ncpoly> | ||
| + | <ncpoly>a1*c*d1*f-b1*c*e1*f</ncpoly> | ||
| + | <ncpoly>a2*c*d2*f-b2*c*e2*f</ncpoly> | ||
| + | <ncpoly>a1*b2*d1*e2-1</ncpoly> | ||
| + | <ncpoly>a2*b1*d2*e1-1</ncpoly> | ||
| + | </basis> | ||
| + | <Comment>Heisenberg_group_2</Comment> | ||
| + | </FREEALGEBRA> | ||
| + | =====Heisenberg group 3===== | ||
| + | <FREEALGEBRA createdAt="2014-03-04" createdBy="strohmeier"> | ||
| + | <vars>a1,a2,a3,b1,b2,b3,c,d1,d2,d3,e1,e2,e3,f</vars> | ||
| + | <uptoDeg>4</uptoDeg> | ||
| + | <basis> | ||
| + | <ncpoly>c*f-1</ncpoly> | ||
| + | <ncpoly>f*c-1</ncpoly> | ||
| + | <ncpoly>a1*d1-1</ncpoly> | ||
| + | <ncpoly>d1*a1-1</ncpoly> | ||
| + | <ncpoly>b1*e1-1</ncpoly> | ||
| + | <ncpoly>e1*b1-1</ncpoly> | ||
| + | <ncpoly>a2*d2-1</ncpoly> | ||
| + | <ncpoly>d2*a2-1</ncpoly> | ||
| + | <ncpoly>b2*e2-1</ncpoly> | ||
| + | <ncpoly>e2*b2-1</ncpoly> | ||
| + | <ncpoly>a3*d3-1</ncpoly> | ||
| + | <ncpoly>d3*a3-1</ncpoly> | ||
| + | <ncpoly>b3*e3-1</ncpoly> | ||
| + | <ncpoly>e3*b3-1</ncpoly> | ||
| + | <ncpoly>a1*b1*d1*e1-c</ncpoly> | ||
| + | <ncpoly>a2*b2*d2*e2-c</ncpoly> | ||
| + | <ncpoly>a3*b3*d3*e3-c</ncpoly> | ||
| + | <ncpoly>a1*c*d1*f-b1*c*e1*f</ncpoly> | ||
| + | <ncpoly>a2*c*d2*f-b2*c*e2*f</ncpoly> | ||
| + | <ncpoly>a3*c*d3*f-b3*c*e3*f</ncpoly> | ||
| + | <ncpoly>a1*b2*d1*e2-1</ncpoly> | ||
| + | <ncpoly>a1*b3*d1*e3-1</ncpoly> | ||
| + | <ncpoly>a2*b1*d2*e1-1</ncpoly> | ||
| + | <ncpoly>a2*b3*d2*e3-1</ncpoly> | ||
| + | <ncpoly>a3*b1*d3*e1-1</ncpoly> | ||
| + | <ncpoly>a3*b2*d3*e2-1</ncpoly> | ||
| + | </basis> | ||
| + | <Comment>Heisenberg_group_3</Comment> | ||
| + | </FREEALGEBRA> | ||
Latest revision as of 20:49, 22 April 2014
Description
The Heisenberg group is the group of 3x3 upper triangular matrices of the form
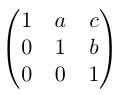
Heisenberg groups are often used in quantum mechanics and also occurs in fourier analysis. A representation is given by:
H(2k+1) = <a_{1},...,a_{k},b_{1},...,b_{k},c | [a_{i},b_{i}] = c, [a_{i},c] = [b_{i},c], [a_{i},b_{j}] = 1 for all i != j
Reference
Ernst Binz and Sonja Pods, Geometry of Heisenberg Groups, American Mathematical Society, 2008.
Computation
/*Use the ApCoCoA package ncpoly.*/
// Number of Heisenberg group
MEMORY.N:=1;
// a invers to d and b invers to e and c invers to f
Use ZZ/(2)[a[1..MEMORY.N],b[1..MEMORY.N],c,d[1..MEMORY.N],e[1..MEMORY.N],f];
NC.SetOrdering("LLEX");
Define CreateRelationsHeisenberg()
Relations:=[];
// add the relations of the inverse elements ad = da = be = eb = cf = fc = 1
Append(Relations,[[c,f],[1]]);
Append(Relations,[[f,c],[1]]);
For Index1 := 1 To MEMORY.N Do
Append(Relations,[[a[Index1],d[Index1]],[1]]);
Append(Relations,[[d[Index1],a[Index1]],[1]]);
Append(Relations,[[b[Index1],e[Index1]],[1]]);
Append(Relations,[[e[Index1],b[Index1]],[1]]);
EndFor;
// add the relation [a_{i}, b_{i}] = c
For Index2 := 1 To MEMORY.N Do
Append(Relations,[[a[Index2],b[Index2],d[Index2],e[Index2]],[c]]);
EndFor;
// add the relation [a_{i}, c] = [b_i, c]
For Index3 := 1 To MEMORY.N Do
Append(Relations,[[a[Index3],c,d[Index3],f],[b[Index3],c,e[Index3],f]]);
EndFor;
// add the relation [a_{i}, b_{j}] = 1 for all i != j
For Index4 := 1 To MEMORY.N Do
For Index5 := 1 To MEMORY.N Do
If Index4 <> Index5 Then
Append(Relations,[[a[Index4],b[Index5],d[Index4],e[Index5]],[1]]);
EndIf;
Endfor;
EndFor;
Return Relations;
EndDefine;
Relations:=CreateRelationsHeisenberg();
Relations;
Size(Relations);
Gb:=NC.GB(Relations,31,1,100,1000);
Size(Gb);
Examples in Symbolic Data Format
Heisenberg group 1
<FREEALGEBRA createdAt="2014-03-04" createdBy="strohmeier"> <vars>a1,b1,c,d1,e1,f</vars> <uptoDeg>7</uptoDeg> <basis> <ncpoly>c*f-1</ncpoly> <ncpoly>f*c-1</ncpoly> <ncpoly>a1*d1-1</ncpoly> <ncpoly>d1*a1-1</ncpoly> <ncpoly>b1*e1-1</ncpoly> <ncpoly>e1*b1-1</ncpoly> <ncpoly>a1*b1*d1*e1-c</ncpoly> <ncpoly>a1*c*d1*f-b1*c*e1*f</ncpoly> </basis> <Comment>Heisenberg_group_1</Comment> </FREEALGEBRA>
Heisenberg group 2
<FREEALGEBRA createdAt="2014-03-04" createdBy="strohmeier"> <vars>a1,a2,b1,b2,c,d1,d2,e1,e2,f</vars> <uptoDeg>5</uptoDeg> <basis> <ncpoly>c*f-1</ncpoly> <ncpoly>f*c-1</ncpoly> <ncpoly>a1*d1-1</ncpoly> <ncpoly>d1*a1-1</ncpoly> <ncpoly>b1*e1-1</ncpoly> <ncpoly>e1*b1-1</ncpoly> <ncpoly>a2*d2-1</ncpoly> <ncpoly>d2*a2-1</ncpoly> <ncpoly>b2*e2-1</ncpoly> <ncpoly>e2*b2-1</ncpoly> <ncpoly>a1*b1*d1*e1-c</ncpoly> <ncpoly>a2*b2*d2*e2-c</ncpoly> <ncpoly>a1*c*d1*f-b1*c*e1*f</ncpoly> <ncpoly>a2*c*d2*f-b2*c*e2*f</ncpoly> <ncpoly>a1*b2*d1*e2-1</ncpoly> <ncpoly>a2*b1*d2*e1-1</ncpoly> </basis> <Comment>Heisenberg_group_2</Comment> </FREEALGEBRA>
Heisenberg group 3
<FREEALGEBRA createdAt="2014-03-04" createdBy="strohmeier"> <vars>a1,a2,a3,b1,b2,b3,c,d1,d2,d3,e1,e2,e3,f</vars> <uptoDeg>4</uptoDeg> <basis> <ncpoly>c*f-1</ncpoly> <ncpoly>f*c-1</ncpoly> <ncpoly>a1*d1-1</ncpoly> <ncpoly>d1*a1-1</ncpoly> <ncpoly>b1*e1-1</ncpoly> <ncpoly>e1*b1-1</ncpoly> <ncpoly>a2*d2-1</ncpoly> <ncpoly>d2*a2-1</ncpoly> <ncpoly>b2*e2-1</ncpoly> <ncpoly>e2*b2-1</ncpoly> <ncpoly>a3*d3-1</ncpoly> <ncpoly>d3*a3-1</ncpoly> <ncpoly>b3*e3-1</ncpoly> <ncpoly>e3*b3-1</ncpoly> <ncpoly>a1*b1*d1*e1-c</ncpoly> <ncpoly>a2*b2*d2*e2-c</ncpoly> <ncpoly>a3*b3*d3*e3-c</ncpoly> <ncpoly>a1*c*d1*f-b1*c*e1*f</ncpoly> <ncpoly>a2*c*d2*f-b2*c*e2*f</ncpoly> <ncpoly>a3*c*d3*f-b3*c*e3*f</ncpoly> <ncpoly>a1*b2*d1*e2-1</ncpoly> <ncpoly>a1*b3*d1*e3-1</ncpoly> <ncpoly>a2*b1*d2*e1-1</ncpoly> <ncpoly>a2*b3*d2*e3-1</ncpoly> <ncpoly>a3*b1*d3*e1-1</ncpoly> <ncpoly>a3*b2*d3*e2-1</ncpoly> </basis> <Comment>Heisenberg_group_3</Comment> </FREEALGEBRA>