ApCoCoA-1:Ap Tutorial De Example: Difference between revisions
New page: Example |
No edit summary |
||
| Line 1: | Line 1: | ||
== Ein rundes Beispiel == | |||
Zuallererst konstruieren wir uns eine gestörte Menge von Punkten. Hierfür verwenden wir in '''ApCoCoA''' die folgenden kleinen Programme. | |||
Mit Hilfe der Befehle | |||
<code> | |||
M:=Mat([[0.9817,-0.191],[0.191,0.9817]]); | |||
U:=[]; | |||
P:=Mat([[1],[0]]); | |||
For I:=1 To 500 Do | |||
P:=M*P; | |||
P[1,1]:=FloatApprox(P[1,1],\,10\^{}(-6)); | |||
P[2,1]:=FloatApprox(P[2,1],\,10\^{}(-6)); | |||
Append(U,\,[P[1,1],\,P[2,1]]); | |||
EndFor; | |||
</code> | |||
erzeugen wir zunächst 500 Punkte, die in der Nähe des Einheitskreises liegen. | |||
Hierbei wird der Punkt <math>(1,0)</math> jeweils um ca. <math>11^\circ</math> | |||
weitergedreht. Dann betrachten wir die Kreise vom Radius <math>\sqrt{2}</math> um den Punkt <math>(2,2,2)</math>, | |||
die in den Ebenen <math>E_1: x-z=0</math> und <math>E_2: x+y-z=6</math> liegen. Mit | |||
<code> | |||
A:=[[2+P[2],2+P[1]*1.414,2+P[2]]|P In U]; | |||
B:=[[2+P[1]+P[2]*0.577,\,2-2*P[2]*0.577,\,2-P[1]+P[2]*0.577]\,|\,P In U]; | |||
C:=Mat(Concat(A,B)); | |||
</code> | |||
erzeugen wir dann 1000 Punkte, die wie zwei Gürtel stark gestört | |||
um die beiden Kreise liegen. | |||
<center>[[Image:1000Punkte.png]]</center> | |||
Nun suchen wir nach polynomialen Relationen, die | |||
an diesen Punkten approximativ verschwinden. Wir machen über | |||
die Gestalt der zu berechnenden Gleichungen nur geringe Annahmen: | |||
Die in den Relationen vorkommenden Variablen seien bekannt, | |||
und die gesuchten Relationen seien von polynomialer Natur. | |||
Der ApCoCoA-Befehl | |||
<center></tt>L:=Numerical.GBasisOfPoints(C,0.08,False);</tt></center> | |||
berechnet eine sogenannte Gröbner-Basis des approximativen | |||
Verschwindungsideals der 1000 Punkte, wobei <math>\varepsilon=0.08</math> | |||
verwendet wird. Die resultierende Liste <math>L=[f_1,f_2,\dots]</math> | |||
enthält Polynome <math>f_1</math> und <math>f_2</math> mit | |||
<center><math>f_1 \approx -0.07x^2-0.07y^2-0.07z^2+0.29x+0.29y+0.29z-0.71</math></center> | |||
und | |||
<center><math>f_1-2.3\cdot f_2 \approx -0.07x^2-0.07xy+0.07yz+0.07z^2+0.43x-0.43z</math></center> | |||
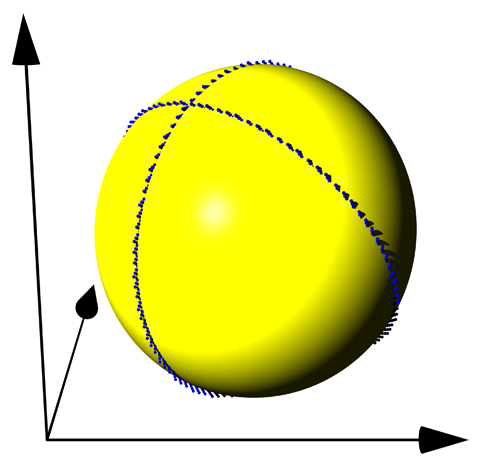
Das erste ist ziemlich genau das <math>-0.07</math>-fache der definierenden | |||
Gleichung der Sphäre | |||
<center><math>\left(x-2\right)^2+\left(y-2\right)^2+\left(z-2\right)^2=2</math></center> | |||
und das zweite entspricht der Gleichung | |||
<center><math>\left(x-z\right)\left(x+y+z-6\right)=0</math></center> | |||
der beiden Ebenen, die wir ja zur Konstruktion der Punkte verwendet hatten. | |||
<center>[[Image:1000Punkte_Sphere.png]]</center> | |||
[[Category:Tutorial_De|Example]] | [[Category:Tutorial_De|Example]] | ||
Revision as of 10:23, 18 July 2008
Ein rundes Beispiel
Zuallererst konstruieren wir uns eine gestörte Menge von Punkten. Hierfür verwenden wir in ApCoCoA die folgenden kleinen Programme.
Mit Hilfe der Befehle
M:=Mat([[0.9817,-0.191],[0.191,0.9817]]);
U:=[];
P:=Mat([[1],[0]]);
For I:=1 To 500 Do
P:=M*P;
P[1,1]:=FloatApprox(P[1,1],\,10\^{}(-6));
P[2,1]:=FloatApprox(P[2,1],\,10\^{}(-6));
Append(U,\,[P[1,1],\,P[2,1]]);
EndFor;
erzeugen wir zunächst 500 Punkte, die in der Nähe des Einheitskreises liegen. Hierbei wird der Punkt jeweils um ca. weitergedreht. Dann betrachten wir die Kreise vom Radius um den Punkt , die in den Ebenen und liegen. Mit
A:=[[2+P[2],2+P[1]*1.414,2+P[2]]|P In U];
B:=[[2+P[1]+P[2]*0.577,\,2-2*P[2]*0.577,\,2-P[1]+P[2]*0.577]\,|\,P In U];
C:=Mat(Concat(A,B));
erzeugen wir dann 1000 Punkte, die wie zwei Gürtel stark gestört um die beiden Kreise liegen.
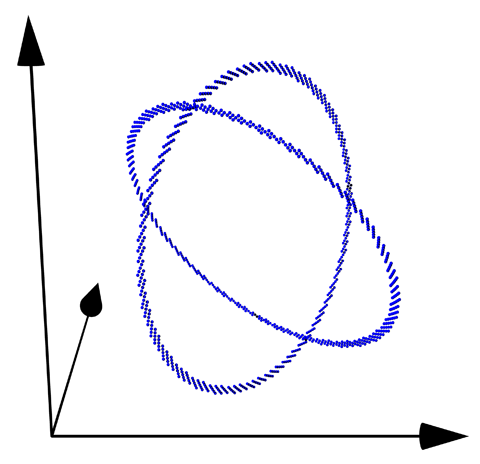
Nun suchen wir nach polynomialen Relationen, die an diesen Punkten approximativ verschwinden. Wir machen über die Gestalt der zu berechnenden Gleichungen nur geringe Annahmen: Die in den Relationen vorkommenden Variablen seien bekannt, und die gesuchten Relationen seien von polynomialer Natur.
Der ApCoCoA-Befehl
berechnet eine sogenannte Gröbner-Basis des approximativen Verschwindungsideals der 1000 Punkte, wobei verwendet wird. Die resultierende Liste enthält Polynome und mit
und
Das erste ist ziemlich genau das -fache der definierenden Gleichung der Sphäre
und das zweite entspricht der Gleichung
der beiden Ebenen, die wir ja zur Konstruktion der Punkte verwendet hatten.