ApCoCoA-1:Fundamentals Tutorial De Ring: Difference between revisions
New page: == Wo bin ich? (... und wie kann ich umziehen?) == In {\CoCoA} rechnet man üblicherweise in einem Polynomring, also idealerweise in Polynomen, welche über einem Körper definiert sin... |
No edit summary |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Wo bin ich? (... und wie kann ich umziehen?) == | == Wo bin ich? (... und wie kann ich umziehen?) == | ||
In CoCoA rechnet man üblicherweise in einem Polynomring, also idealerweise in Polynomen, welche über einem Körper definiert sind. Dieser Körper muss natürlich Computerverträglich sein: <math>\mathbb{R}</math> ist zwar ein schöner Körper, aber für den Einsatz in der Computeralgebra total ungeeignet, da sich Elemente wie <math>\pi</math> und <math>\sqrt{2}</math> nun einfach nicht in endlich vielen Stellen abspeichern lassen. Jedoch wollen wir nicht so schnell aufgeben, symbolisch kann CoCoA}mit dem Objekt <math>\sqrt{2}</math> ohne Probleme umgehen. | |||
Im Gegensatz zu normalen Definitionen werden Ringe mit <tt>::=</tt> festgelegt, so wird der Polynomring <math>\mathbb{F}_5\left[x,y\right]:=\mathbb{Z}/\!\;\!_{5\mathbb{Z}}\left[x,y\right]</math> mit <tt>S::=Z/(5)[x,y];</tt> unter dem Namen <tt>S</tt> bereitgestellt. | |||
Mit <tt>Use S;</tt> wird dann bis auf weiteres auf den neuen Ring umgestellt. Wenn man nur für eine Berechnung umschalten möchte, so kann man das Befehlspaar <tt>Using</tt> und <tt>EndUsing;</tt> verwenden: | |||
<code> | |||
Using S Do | |||
For I:= 1 To Characteristic(S) Do} | |||
I^2; | |||
PrintLn; | |||
EndFor; | |||
EndUsing; | |||
</code> | |||
Wichtig ist hier, dass der Befehl eigentlich aus drei Teilen (<tt>Using</tt>, <tt>Do</tt> und <tt>EndUsing</tt>) besteht und nur ein Semikolon am Ende von <tt>EndUsing</tt> bedarf. | |||
<center>[[Image:1to25.png]]</center> | |||
Die Syntax der <tt>For</tt>-Schleife ist mit der von <Using> vergleichbar und der Befehl <tt>PrintLn;</tt> verursacht einen Zeilenumbruch. Ziemlich vorhersagbar ist der Befehl <tt>Charakteristic(S)</tt>, welcher uns die Charakteristik des Körpers <math>\mathbb{F}_5</math>, also 5 liefert. | |||
Aber eigentlich wollten wir doch modulo rechnen. Das Problem ist nun, das das {\CoCoA} ja nicht ahnen kann, also müssen wir dies explizit angeben: | |||
<code> | |||
Using S Do | |||
For I:= 1 To Characteristic(S) Do | |||
(I^2)%Characteristic(S); | |||
PrintLn; | |||
EndFor; | |||
EndUsing; | |||
</code> | |||
Ohne die runden Klammern um <tt>I^2</tt> funktioniert die Rechnung nicht. Klar, wir wissen ja schon, dass CoCoA nicht raten kann was wir meinen. Wie soll CoCoA entscheiden, ob mit der Eingabe <tt>I^2%Characteristic(S);</tt> nun </tt>(I^2)%Characteristic(S);</tt> oder <tt>I^(2%Characteristic(S));</tt> gemeint ist. | |||
<center>[[Image:1To25modulo.png]]</center> | |||
CoCoA gibt also immer den betragsmäßig kleinsten modulo-Wert aus. | |||
Nach einiger Zeit verliert man schon mal den Überblick, welche Ringe einem zur Verfügung stehen, hier schafft der Befehl <tt>RingEnvs();</tt> Abhilfe. | |||
<center>[[Image:ringenvs.png]]</center> | |||
---- | |||
Weiter geht's im Kapitel [[ApCoCoA:Examples_Tutorial_De_Help|Hilfe - Das CoCoA-Manual]]. | |||
---- | |||
[[Category:Tutorial_De|Ring]] | |||
Latest revision as of 19:10, 17 July 2008
Wo bin ich? (... und wie kann ich umziehen?)
In CoCoA rechnet man üblicherweise in einem Polynomring, also idealerweise in Polynomen, welche über einem Körper definiert sind. Dieser Körper muss natürlich Computerverträglich sein: ist zwar ein schöner Körper, aber für den Einsatz in der Computeralgebra total ungeeignet, da sich Elemente wie und nun einfach nicht in endlich vielen Stellen abspeichern lassen. Jedoch wollen wir nicht so schnell aufgeben, symbolisch kann CoCoA}mit dem Objekt ohne Probleme umgehen.
Im Gegensatz zu normalen Definitionen werden Ringe mit ::= festgelegt, so wird der Polynomring mit S::=Z/(5)[x,y]; unter dem Namen S bereitgestellt.
Mit Use S; wird dann bis auf weiteres auf den neuen Ring umgestellt. Wenn man nur für eine Berechnung umschalten möchte, so kann man das Befehlspaar Using und EndUsing; verwenden:
Using S Do
For I:= 1 To Characteristic(S) Do}
I^2;
PrintLn;
EndFor;
EndUsing;
Wichtig ist hier, dass der Befehl eigentlich aus drei Teilen (Using, Do und EndUsing) besteht und nur ein Semikolon am Ende von EndUsing bedarf.
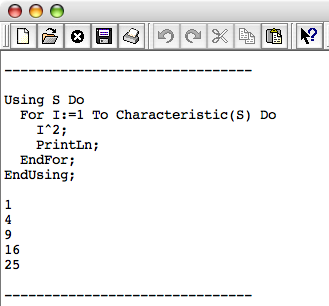
Die Syntax der For-Schleife ist mit der von <Using> vergleichbar und der Befehl PrintLn; verursacht einen Zeilenumbruch. Ziemlich vorhersagbar ist der Befehl Charakteristic(S), welcher uns die Charakteristik des Körpers , also 5 liefert.
Aber eigentlich wollten wir doch modulo rechnen. Das Problem ist nun, das das {\CoCoA} ja nicht ahnen kann, also müssen wir dies explizit angeben:
Using S Do
For I:= 1 To Characteristic(S) Do
(I^2)%Characteristic(S);
PrintLn;
EndFor;
EndUsing;
Ohne die runden Klammern um I^2 funktioniert die Rechnung nicht. Klar, wir wissen ja schon, dass CoCoA nicht raten kann was wir meinen. Wie soll CoCoA entscheiden, ob mit der Eingabe I^2%Characteristic(S); nun (I^2)%Characteristic(S); oder I^(2%Characteristic(S)); gemeint ist.
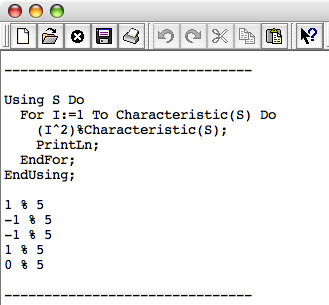
CoCoA gibt also immer den betragsmäßig kleinsten modulo-Wert aus.
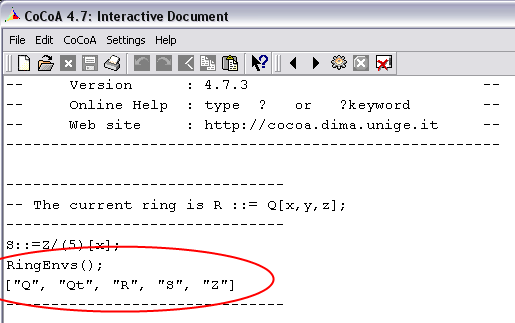
Nach einiger Zeit verliert man schon mal den Überblick, welche Ringe einem zur Verfügung stehen, hier schafft der Befehl RingEnvs(); Abhilfe.
Weiter geht's im Kapitel Hilfe - Das CoCoA-Manual.
