Difference between revisions of "ApCoCoA-1:Examples Tutorial De List"
KHiddemann (talk | contribs) m (ApCoCoA:Exampels Tutorial De List moved to ApCoCoA:Examples Tutorial De List: typo) |
|||
| Line 1: | Line 1: | ||
== Die List mit den Listen == | == Die List mit den Listen == | ||
| + | |||
| + | Der Listenoperator in CoCoA ist ein sehr vielseitiges und auch kräftiges Hilfsmittel. Wenn immer es geht sollte man mit Listen arbeiten, da aufgrund der inneren Struktur von CoCoA auf diese und in ihnen ein sehr schneller Zugriff möglich ist. | ||
| + | |||
| + | Eine Liste ist keine Menge, so ist <math>\texttt{[0,1,3,0]}\neq \texttt{[0,1,3]}</math>. | ||
| + | |||
| + | Man kann, wie vielleicht schon gesehen, Listen einfach durch Aufzählung ihrer Elemente angeben, z.B. | ||
| + | <tt>L:=[0,1,2,3,4,5,6,7,8,9]</tt>. Die Liste trägt nun den Namen <tt>L</tt> und enthält 10 Elemente. Natürlich | ||
| + | geht die Definition der Liste <tt>L</tt> auch einfacher: Der kürzeste Weg ist <tt>L:=0..9;</tt>, was | ||
| + | ebenfalls das Anlegen einer Liste mit den Zahlen von <tt>0</tt> bis <tt>9</tt> in Reihenfolge verursacht. | ||
| + | |||
| + | Die leere Liste wird einfach mit <tt>[]</tt> erzeugt. An eine leere Liste können z.B. mittels <tt>Concat(...)</tt> innerhalb eines Programms immer wieder neue Teile angefügt werden. Wohingegen der Befehl <tt>NL:=NewList(5);</tt> eine Liste mit fünf leeren Plätzen erzeugt, welche dann einzeln belegt werden können. Diese Leerliste hat dann die Gestalt <tt>[Null,Null,Null,Null,Null]</tt>. Auf die einzelnen Elemente von <tt>L</tt> kann man jetzt durch Angabe der Position zugreifen, so liefert <tt>L[3];</tt> die Zahl <tt>2</tt>, also die Zahl, welche an dritter Stelle in der Liste <tt>L</tt> steht. Alternativ kann man auch mit <tt>Comp(L,3)</tt> auf den dritten Eintag von <tt>L</tt> zugreifen. Man kann aber nicht nur Daten aus einer bestimmten Position einer Liste auslesen, sondern genauso an eine bestimmte Position schreiben: So verursacht z.B. <tt>NL[3]:=3;</tt> das an dritter Stelle von <tt>NL</tt> der Wert <tt>3</tt> eingetragen wird: <tt>[Null,Null,3,Null,Null]</tt>. | ||
| + | |||
| + | Wenn man nach einer längeren Konstruktion merkt, dass man etwas in einer Liste vergessen hat, so braucht man nicht alles neu machen. Mit <tt>Insert(L,S,O);</tt> wird in die Liste <tt>L</tt> an die Stelle <tt>S</tt> das Objekt <tt>O</tt> eingesetzt. Sei z.B. <tt>L:=[1,3,7,9];</tt> (irgendwie fehlt da die <tt>5</tt>), dann transformiert <tt>Insert(L,3,5);</tt> die Liste <tt>L</tt> in <tt>[1,3,5,7,9]</tt>. Hat sich nun ein ungewolltes Objekt in eine Liste, wie z.B. die <tt>7</tt> in die Liste <tt>K:=[2,4,6,7,8];</tt> eingeschlichen, so kann man mit <tt>Remove(L,S);</tt> aus der Liste <tt>L</tt> die Stelle <tt>S</tt> wieder entfernen, d.h. <tt>Remove(K,4);</tt> liefert die gewünschte Liste <tt>K=[2,4,6,8]</tt>. | ||
| + | |||
| + | Wenn man neue Listen mit bestimmten Eigenschaften der Inhalte erzeugen möchte so hat man mit CoCoA noch eine Menge Gestaltungsmöglichkeiten, z.B. | ||
| + | <center>[[Image:list_constructor.png]]</center> | ||
| + | Hier wurden aus der Liste der Zahlen von <tt>0</tt> bis <tt>11</tt> die Liste der Quadratzahlen (von <tt>0</tt> bis <tt>11</tt>) modulo <tt>12</tt> erzeugt. | ||
| + | |||
| + | Sei \texttt{L:=1..100;}. Dann erzeugt \texttt{G:=[N In L | Mod(N,2)=0];} die Liste aller geraden Zahlen von 2 bis 100: \texttt{G=[2,4,6,8,...,98,100]}. Mit dem Befehl \texttt{In} kann man angeben, aus welcher Liste die Objekte ausgelesen werden sollen, die Bedingungen/Opertionen werden hinter einem \texttt{|} angegeben. So wir durch \texttt{H:=[N\textasciicircum 2 | N In L];} die Liste aller Zahlen von 1 bis 100 quadriert erzeugt: \texttt{H=[1,4,9,...,10000]}. Wenn man mehr als eine Bedingung angeben möchte, so kann man dies mit Hilfe der Befehle \texttt{And} und \texttt{Or} tun, z.B. erzeugt \texttt{I:=[N\textasciicircum 2 | N In L And N<=10];} die Liste \texttt{I=[1,4,9,...,100]}. | ||
| + | \medskip | ||
| + | |||
| + | Hat man nun Listen in denen wieder Listen vorkommen, wie z.B. \texttt{LL:=[[1,4],3,[[9,7],6]];}, so kann | ||
| + | man mit \texttt{L:=Flatten(LL);} aus der Liste \texttt{LL} die Liste \texttt{L=[1,4,3,9,7,6];} machen. | ||
| + | Der Befehl \texttt{Flatten(...);} hat ein oder zwei Parameter, zuerst die Liste, welche vereinfacht werden | ||
| + | soll und dann ggf. die Stufe der Vereinfachung. Gibt man keine Stufe der Vereinfachung an, so erzeugt | ||
| + | {\CoCoA} die maximale Vereinfachung der Liste. Betrachten wir z.B. die Liste \texttt{M:=[[[1,2],[4,7]],[3,2]]}, | ||
| + | dann verursacht \texttt{Flatten(M,1);} die Vereinfachung der Liste um eine Stufe, wir erhalten | ||
| + | \texttt{M:=[[1,2],[4,7],3,2]}, also wurde eine Stufe der inneren Klammern aufgehoben. Nochmaliges anwenden | ||
| + | von \texttt{Flatten(M,1);} liefert dann die maximale Vereinfachung \texttt{M:=[1,2,4,7,3,2]}. | ||
| + | \medskip | ||
| + | |||
| + | Der Befehl \texttt{Concat(...);} macht aus mehreren Listen eine große Liste, wobei die | ||
| + | erhaltene Liste so viele Stufen hat, wie die eingegebene Liste mit der höchsten Stufenzahl. | ||
| + | So erhält man \texttt{[[4,8,0],[2],1,2]}, wenn man \texttt{L:=Concat([[4,8,0],[2]],[\,],[1,2]);} | ||
| + | in {\CoCoA} ausführt. Wenn man nur ein Objekt an das Ende einer Liste anhängen möchte, so kann man \texttt{Append(L,O);} verwenden. Das Objekt \texttt{O} wird nach dem letzten Objekt der Liste \texttt{L} eingehängt, z.B. wird \texttt{L=[[4,8,0],[2],1,2]} durch \texttt{Append(L,[7,2]);} zu \texttt{L=[[4,8,0],[2],1,2,[7,2]]}. | ||
| + | \begin{center} | ||
| + | \includegraphics[width=0.55\textwidth]{./../images/bsp_listen_1} | ||
| + | \end{center} | ||
| + | |||
| + | Man kann natürlich zwei Listen auch miteinander vergleichen, so liefert \texttt{Diff(L1,L2);} die Liste der Elemente, in denen sich \texttt{L1} und \texttt{L2} unterscheiden. Mit \texttt{First(L,N);} erhält man die Liste der ersten \texttt{N} Elemente von \texttt{L} und mit \texttt{Last(L,N);} die Liste der letzten \texttt{N} Elemente von \texttt{L}. Braucht man mal die Länge einer Liste \texttt{L}, so liefert \texttt{Len(L);} die Antwort. | ||
| + | \begin{center} | ||
| + | \includegraphics[width=0.45\textwidth]{./../images/bsp_listen_2} | ||
| + | \end{center} | ||
Revision as of 12:57, 17 July 2008
Die List mit den Listen
Der Listenoperator in CoCoA ist ein sehr vielseitiges und auch kräftiges Hilfsmittel. Wenn immer es geht sollte man mit Listen arbeiten, da aufgrund der inneren Struktur von CoCoA auf diese und in ihnen ein sehr schneller Zugriff möglich ist.
Eine Liste ist keine Menge, so ist .
Man kann, wie vielleicht schon gesehen, Listen einfach durch Aufzählung ihrer Elemente angeben, z.B. L:=[0,1,2,3,4,5,6,7,8,9]. Die Liste trägt nun den Namen L und enthält 10 Elemente. Natürlich geht die Definition der Liste L auch einfacher: Der kürzeste Weg ist L:=0..9;, was ebenfalls das Anlegen einer Liste mit den Zahlen von 0 bis 9 in Reihenfolge verursacht.
Die leere Liste wird einfach mit [] erzeugt. An eine leere Liste können z.B. mittels Concat(...) innerhalb eines Programms immer wieder neue Teile angefügt werden. Wohingegen der Befehl NL:=NewList(5); eine Liste mit fünf leeren Plätzen erzeugt, welche dann einzeln belegt werden können. Diese Leerliste hat dann die Gestalt [Null,Null,Null,Null,Null]. Auf die einzelnen Elemente von L kann man jetzt durch Angabe der Position zugreifen, so liefert L[3]; die Zahl 2, also die Zahl, welche an dritter Stelle in der Liste L steht. Alternativ kann man auch mit Comp(L,3) auf den dritten Eintag von L zugreifen. Man kann aber nicht nur Daten aus einer bestimmten Position einer Liste auslesen, sondern genauso an eine bestimmte Position schreiben: So verursacht z.B. NL[3]:=3; das an dritter Stelle von NL der Wert 3 eingetragen wird: [Null,Null,3,Null,Null].
Wenn man nach einer längeren Konstruktion merkt, dass man etwas in einer Liste vergessen hat, so braucht man nicht alles neu machen. Mit Insert(L,S,O); wird in die Liste L an die Stelle S das Objekt O eingesetzt. Sei z.B. L:=[1,3,7,9]; (irgendwie fehlt da die 5), dann transformiert Insert(L,3,5); die Liste L in [1,3,5,7,9]. Hat sich nun ein ungewolltes Objekt in eine Liste, wie z.B. die 7 in die Liste K:=[2,4,6,7,8]; eingeschlichen, so kann man mit Remove(L,S); aus der Liste L die Stelle S wieder entfernen, d.h. Remove(K,4); liefert die gewünschte Liste K=[2,4,6,8].
Wenn man neue Listen mit bestimmten Eigenschaften der Inhalte erzeugen möchte so hat man mit CoCoA noch eine Menge Gestaltungsmöglichkeiten, z.B.
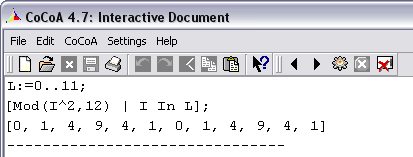
Hier wurden aus der Liste der Zahlen von 0 bis 11 die Liste der Quadratzahlen (von 0 bis 11) modulo 12 erzeugt.
Sei \texttt{L:=1..100;}. Dann erzeugt \texttt{G:=[N In L | Mod(N,2)=0];} die Liste aller geraden Zahlen von 2 bis 100: \texttt{G=[2,4,6,8,...,98,100]}. Mit dem Befehl \texttt{In} kann man angeben, aus welcher Liste die Objekte ausgelesen werden sollen, die Bedingungen/Opertionen werden hinter einem \texttt{|} angegeben. So wir durch \texttt{H:=[N\textasciicircum 2 | N In L];} die Liste aller Zahlen von 1 bis 100 quadriert erzeugt: \texttt{H=[1,4,9,...,10000]}. Wenn man mehr als eine Bedingung angeben möchte, so kann man dies mit Hilfe der Befehle \texttt{And} und \texttt{Or} tun, z.B. erzeugt \texttt{I:=[N\textasciicircum 2 | N In L And N<=10];} die Liste \texttt{I=[1,4,9,...,100]}. \medskip
Hat man nun Listen in denen wieder Listen vorkommen, wie z.B. \texttt{LL:=[[1,4],3,[[9,7],6]];}, so kann man mit \texttt{L:=Flatten(LL);} aus der Liste \texttt{LL} die Liste \texttt{L=[1,4,3,9,7,6];} machen. Der Befehl \texttt{Flatten(...);} hat ein oder zwei Parameter, zuerst die Liste, welche vereinfacht werden soll und dann ggf. die Stufe der Vereinfachung. Gibt man keine Stufe der Vereinfachung an, so erzeugt {\CoCoA} die maximale Vereinfachung der Liste. Betrachten wir z.B. die Liste \texttt{M:=[[[1,2],[4,7]],[3,2]]}, dann verursacht \texttt{Flatten(M,1);} die Vereinfachung der Liste um eine Stufe, wir erhalten \texttt{M:=[[1,2],[4,7],3,2]}, also wurde eine Stufe der inneren Klammern aufgehoben. Nochmaliges anwenden von \texttt{Flatten(M,1);} liefert dann die maximale Vereinfachung \texttt{M:=[1,2,4,7,3,2]}. \medskip
Der Befehl \texttt{Concat(...);} macht aus mehreren Listen eine große Liste, wobei die erhaltene Liste so viele Stufen hat, wie die eingegebene Liste mit der höchsten Stufenzahl. So erhält man \texttt{[[4,8,0],[2],1,2]}, wenn man \texttt{L:=Concat([[4,8,0],[2]],[\,],[1,2]);} in {\CoCoA} ausführt. Wenn man nur ein Objekt an das Ende einer Liste anhängen möchte, so kann man \texttt{Append(L,O);} verwenden. Das Objekt \texttt{O} wird nach dem letzten Objekt der Liste \texttt{L} eingehängt, z.B. wird \texttt{L=[[4,8,0],[2],1,2]} durch \texttt{Append(L,[7,2]);} zu \texttt{L=[[4,8,0],[2],1,2,[7,2]]}. \begin{center} \includegraphics[width=0.55\textwidth]{./../images/bsp_listen_1} \end{center}
Man kann natürlich zwei Listen auch miteinander vergleichen, so liefert \texttt{Diff(L1,L2);} die Liste der Elemente, in denen sich \texttt{L1} und \texttt{L2} unterscheiden. Mit \texttt{First(L,N);} erhält man die Liste der ersten \texttt{N} Elemente von \texttt{L} und mit \texttt{Last(L,N);} die Liste der letzten \texttt{N} Elemente von \texttt{L}. Braucht man mal die Länge einer Liste \texttt{L}, so liefert \texttt{Len(L);} die Antwort. \begin{center} \includegraphics[width=0.45\textwidth]{./../images/bsp_listen_2} \end{center}
![{\displaystyle {\texttt {[0,1,3,0]}}\neq {\texttt {[0,1,3]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ba98cec676adb24ff38437b96f318618e5a849a)